Условие задачи:
Амперметр с внутренним сопротивлением 2 Ом, подключенный к батарее, показывает ток 5 А. Вольтметр с внутренним сопротивлением 150 Ом, подключенный к той же батарее, показывает 12 В. Найти ток короткого замыкания батареи.
Задача №7.5.24 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(R_А=2\) Ом, \(I_1=5\) А, \(R_v=150\) Ом, \(U_2=12\) В, \(I_{кз}-?\)
Решение задачи:
 Ток короткого замыкания батареи \(I_{кз}\) определяют по следующей формуле:
Ток короткого замыкания батареи \(I_{кз}\) определяют по следующей формуле:
\[{I_{кз}} = \frac{{\rm E}}{r}\;\;\;\;(1)\]
Получается, что нам необходимо найти ЭДС батареи \(\rm E\) и ее внутреннее сопротивление \(r\).
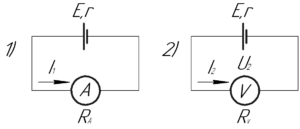
Запишем закон Ома для полной цепи применительно к первому и второму случаю (см. рисунки 1 и 2):
\[\left\{ \begin{gathered}
{I_1} = \frac{{\rm E}}{{{R_А} + r}} \hfill \\
{I_2} = \frac{{\rm E}}{{{R_v} + r}} \hfill \\
\end{gathered} \right.\]
Напряжение на вольтметре во втором случае \(U_2\) легко определить по формуле:
\[{U_2} = {I_2}{R_v}\]
Учитывая вышеприведенное выражение в системе для нахождения силы тока \(I_2\), получим:
\[{U_2} = \frac{{{\rm E}{R_v}}}{{{R_v} + r}}\]
Имеем такую систему с двумя неизвестными:
\[\left\{ \begin{gathered}
{I_1} = \frac{{\rm E}}{{{R_А} + r}} \hfill \\
{U_2} = \frac{{{\rm E}{R_v}}}{{{R_v} + r}} \hfill \\
\end{gathered} \right.\]
Из первого уравнения выразим ЭДС:
\[{\rm E} = {I_1}\left( {{R_А} + r} \right)\;\;\;\;(2)\]
Подставим полученное во второе уравнение:
\[{U_2} = \frac{{{I_1}{R_v}\left( {{R_А} + r} \right)}}{{{R_v} + r}}\]
Тогда:
\[{U_2}\left( {{R_v} + r} \right) = {I_1}{R_v}\left( {{R_А} + r} \right)\]
Раскроем скобки в обеих частях уравнения, сгруппируем члены с внутренним сопротивлением \(r\) в одной части, чтобы далее выразить его:
\[{U_2}{R_v} + {U_2}r = {I_1}{R_v}{R_А} + {I_1}{R_v}r\]
\[{U_2}{R_v} — {I_1}{R_v}{R_А} = {I_1}{R_v}r — {U_2}r\]
\[{R_v}\left( {{U_2} — {I_1}{R_А}} \right) = r\left( {{I_1}{R_v} — {U_2}} \right)\]
\[r = \frac{{{R_v}\left( {{U_2} — {I_1}{R_А}} \right)}}{{{I_1}{R_v} — {U_2}}}\;\;\;\;(3)\]
Отлично, полученное выражение подставим в (2), чтобы найти ЭДС:
\[{\rm E} = {I_1}\left( {{R_А} + \frac{{{R_v}\left( {{U_2} — {I_1}{R_А}} \right)}}{{{I_1}{R_v} — {U_2}}}} \right)\]
Приведем в скобках под общий знаменатель:
\[{\rm E} = {I_1}\frac{{{R_А}\left( {{I_1}{R_v} — {U_2}} \right) + {R_v}\left( {{U_2} — {I_1}{R_А}} \right)}}{{{I_1}{R_v} — {U_2}}}\]
\[{\rm E} = {I_1}\frac{{{I_1}{R_А}{R_v} — {U_2}{R_А} + {U_2}{R_v} — {I_1}{R_А}{R_v}}}{{{I_1}{R_v} — {U_2}}}\]
\[{\rm E} = \frac{{{I_1}{U_2}\left( {{R_v} — {R_А}} \right)}}{{{I_1}{R_v} — {U_2}}}\;\;\;\;(4)\]
Подставим (3) и (4) в формулу (1), получим решение задачи в общем виде:
\[{I_{кз}} = \frac{{{I_1}{U_2}\left( {{R_v} — {R_А}} \right) \cdot \left( {{I_1}{R_v} — {U_2}} \right)}}{{\left( {{I_1}{R_v} — {U_2}} \right) \cdot {R_v}\left( {{U_2} — {I_1}{R_А}} \right)}}\]
\[{I_{кз}} = \frac{{{I_1}{U_2}\left( {{R_v} — {R_А}} \right)}}{{{R_v}\left( {{U_2} — {I_1}{R_А}} \right)}}\]
Численный ответ задачи равен:
\[{I_{кз}} = \frac{{5 \cdot 12 \cdot \left( {150 — 2} \right)}}{{150 \cdot \left( {12 — 5 \cdot 2} \right)}} = 29,6\;А\]
Ответ: 29,6 А.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
7.5.23 Вольтметр, соединенный последовательно с сопротивлением R1=10 кОм, при включении
7.5.25 Вольтметр, подключенный к источнику с ЭДС 12 В, показывает напряжение 9 В. К его клеммам
7.5.26 Аккумулятор замкнут на некоторый проводник. Если в цепь включить два амперметра

 icodepro.ru
icodepro.ru