icodepro.ruУсловие задачи:
Автобус движется равнозамедленно, проходя при этом до остановки расстояние 310 м. Его начальная скорость 15 м/с. Определить модуль вектора ускорения.
Задача №1.3.11 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(S=310\) м, \(\upsilon_0=15\) м/с, \(a-?\)
Решение задачи:
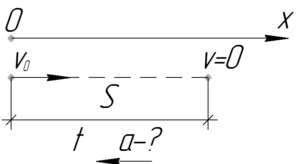Очевидно, что когда автобус остановится, то его скорость \(\upsilon\) будет равна нулю. Воспользуемся следующей известной формулой:
\[{\upsilon ^2} — \upsilon _0^2 = — 2aS\]
Знак «минус» в правой части показывает, что движение является замедленным. Так как конечная скорость \(\upsilon\) отсутствует, то верхнее выражение примет вид:
\[ — \upsilon _0^2 = — 2aS\]
\[\upsilon _0^2 = 2aS\]
Значит, модуль ускорения найдется по формуле:
\[a = \frac{{\upsilon _0^2}}{{2S}}\]
\[a = \frac{{{{15}^2}}}{{2 \cdot 310}} = 0,36\; м/с^2\]
Ответ: 0,36 м/с2.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.3.10 Мотоциклист, подъезжая к уклону, имеет скорость 10 м/с и начинает двигаться
1.3.12 Вычислить тормозной путь автомобиля, имеющего начальную скорость 60 км/ч
1.3.13 Машинист локомотива, движущегося со скоростью 72 км/ч, начал тормозить
Здравствуйте, помогите решить эту задачу. На пути 30 метров скорость уменьшилась в 4 раза. Чему равно весь путь до остановки.
\[\left\{ \begin{gathered}
\upsilon _1^2 — \upsilon _0^2 = — 2a{S_1} \hfill \\
— \upsilon _0^2 = — 2aS \hfill \\
\end{gathered} \right.\]
Так как \({\upsilon _1} = \frac{{{\upsilon _0}}}{4}\), то:\[\left\{ \begin{gathered}
\frac{{\upsilon _0^2}}{{16}} — \upsilon _0^2 = — 2a{S_1} \hfill \\
\upsilon _0^2 = 2aS \hfill \\
\end{gathered} \right.\]\[\left\{ \begin{gathered}
\frac{{15\upsilon _0^2}}{{16}} = 2a{S_1} \hfill \\
\upsilon _0^2 = 2aS \hfill \\
\end{gathered} \right.\]
Тогда:\[\frac{S}{{{S_1}}} = \frac{{16}}{{15}}\]\[S = \frac{{16}}{{15}}{S_1}\]\[S = \frac{{16}}{{15}} \cdot 30 = 32\;м\]
У вас ошибка в решение, в условие говориться про автобус, а в решение у вас почему то поезд)
Действительно, исправил ошибку!
а как решить находя время?
Очень просто:
\(t = \frac{{{\upsilon _0}}}{a}\)
Ускорение мы уже нашли в ходе решения:
\(a = \frac{{\upsilon _0^2}}{{2S}}\)
Тогда:
\(t = \frac{{{\upsilon _0} \cdot 2S}}{{\upsilon _0^2}} = \frac{{2S}}{{{\upsilon _0}}}\)
А куда делось u^2 из 1 формулы?
Конечная скорость ? равна 0