Условие задачи:

Автомобиль, двигаясь равноускоренно, прошел два смежных участка пути по 100 м каждый за 5 с и 3,5 с. Какова средняя скорость на двух участках вместе?

Задача №1.3.30 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(S_1=S_2=100\) м, \(t_1=5\) с, \(t_2=3,5\) с, \(\upsilon_{ср}-?\)

Решение задачи:

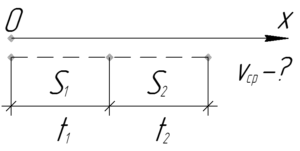Найти среднюю скорость — проще простого! Необходимо весь пройденный путь разделить на все время, потраченное на прохождение этого пути. Применительно к этой задаче в виде формулы это будет выглядеть следующим образом:

\[{\upsilon _{ср}} = \frac{{{S_1} + {S_2}}}{{{t_1} + {t_2}}}\]

Подставим числа в формулу, вычислим ответ:

\[{\upsilon _{ср}} = \frac{{100 + 100}}{{5 + 3,5}} = 23,5\; м/с = 84,7\; км/ч\]

Ответ: 84,7 км/ч.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

1.3.29 Автомобиль начал двигаться с ускорением 1,5 м/с2 и через некоторое время
1.3.31 За первую секунду равноускоренного движения тело проходит путь 1 м, а за
1.3.32 За седьмую секунду равноускоренного движения модуль вектора скорости