Условие задачи:
Баскетболист бросает мяч в кольцо. Скорость мяча после броска 8 м/с и составляет 60° с горизонтом. С какой скоростью мяч попал в кольцо, если он долетел до него за секунду?
Задача №1.6.2 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(v_0=8\) м/с, \(\alpha=60^\circ\), \(t=1\) с, \(v-?\)
Решение:
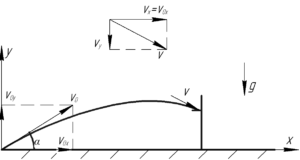 Все понимают, что баскетболист забивает мяч сверху, поэтому рисунок, поясняющий решение данной задачи, выглядит следующим образом (см. справа, клик — для увеличения).
Все понимают, что баскетболист забивает мяч сверху, поэтому рисунок, поясняющий решение данной задачи, выглядит следующим образом (см. справа, клик — для увеличения).
Скорость \(v\) (см. рисунок) в момент попадания мяча в кольцо можно представить в виде двух взаимно перпендикулярных составляющих \(v_x\), равной \(v_{0x}\), поскольку движение вдоль оси \(x\) является равномерным, и \(v_y\), значение которой можно найти из формулы:
\[{v_y} = {v_{0y}} — gt = {v_0}\sin \alpha — gt\]
Если подставить данное нам время полета \(t=1\) с, то мы получим отрицательное значение составляющей скорости \(v_y\), что и понятно, поскольку она должна быть направлена вниз, о чем и говорит этот знак «минус». Никаких действий по избавлению от этого знака «минус» производить не нужно, поскольку в дальнейшем решении в теореме Пифагора составляющая будет использоваться только в квадрате.
Составляющая \(v_x\) определим таким образом:
\[{v_x} = {v_{ox}} = {v_0}\cos \alpha \]
Поэтому, для нахождения скорости \(v\), применим теорему Пифагора и получим формулу для получения ответа в общем виде:
\[v = \sqrt {v_{0x}^2 + v_{0y}^2} = \sqrt {v_0^2{{\cos }^2}\alpha + {{\left( {{v_0}\sin \alpha — gt} \right)}^2}} \]
Подставим все известные данные в системе измерения СИ и, выполнив все действия, получаем ответ:
\[v = \sqrt {{8^2} \cdot {{\cos }^2}60^\circ + {{\left( {8 \cdot \sin 60^\circ — 10 \cdot 1} \right)}^2}} = 5,04\; м/с = 18,16\; км/ч\]
Ответ: 18,16 км/ч.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Если Вам понравилась задача и ее решение, то Вы можете поделитесь ею с друзьями с помощью этих кнопок.
Смотрите также задачи:
1.6.1 Тело брошено со скоростью 10 м/с под углом 30 градусов к горизонту
1.6.3 Камень, брошенный с земли под углом 45 градусов к горизонту
1.6.4 Минимальная скорость при движении тела, брошенного под углом

 icodepro.ru
icodepro.ru
Спасибо за хорошее и понятное решение
Рисунок к задаче не объясняет решение, а, скорей всего, поясняет решение. И такого косноязычия у автора решений полным полно!
Спасибо за замечание, исправлено!
Да, на сайте полно косноязычия, а также ошибок в решениях, я далеко не идеален