Условие задачи:

Брусок массой 3 кг находится на наклонной плоскости, составляющей угол 45° с горизонтом. Какую наименьшую горизонтальную силу следует приложить к бруску, чтобы он покоился, если коэффициент трения между бруском и плоскостью равен 0,5?

Задача №2.3.11 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$m=3$ кг, $\alpha=45^\circ$, $\mu=0,5$, $F-?$

Решение задачи:

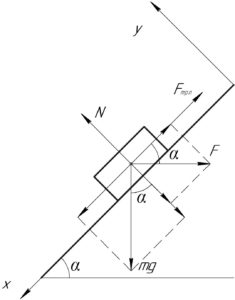Нарисуем схему к задаче, на которой покажем систему координат. Брусок стремиться соскользнуть вниз по оси $x$, значит сила трения покоя направлена против этой оси. Наверное и так понятно, что проекция силы тяжести на ось $x$ больше максимальной силы трения покоя (она равна силе трения скольжения, но брусок ещё покоится), иначе бы вопрос задачи бы бы бессмысленным — брусок и так бы покоился. Проверьте это сами, это будет полезно.

Получается, что мы дополнительно прикладываем к бруску горизонтальную силу $F$, проекция которой на ось $x$ будет направлена против нее. Тогда по первому закону Ньютона:

$$mg \cdot \sin \alpha — F \cdot \cos \alpha — {F_{тр.п}} = 0\;\;\;\;(1)$$

Максимальная сила трения покоя определяется по формуле:

$${F_{тр.п}} = \mu N\;\;\;\;(2)$$

Почему сила трения покоя должна быть максимальной? Это условие минимальности приложенной силы $F$. Т.е. сила трения покоя должна принять своё максимальное значение, чтобы сила $F$ была минимальной. Чтобы это увидеть явно, выразите из формулы (1) силу $F$ — Вы заметите, что когда сила трения максимальна, сила $F$ принимает минимальное значение.

Брусок вдоль оси $y$ не движется, поэтому по первому закону Ньютона в проекции на эту ось:

$$N = mg \cdot \cos \alpha + F \cdot \sin \alpha \;\;\;\;(3)$$

Подставим (3) в (2), а полученное в (1), тогда имеем:

$$mg \cdot \sin \alpha — F \cdot \cos \alpha — \mu \left( {mg \cdot \cos \alpha + F \cdot \sin \alpha } \right) = 0$$

$$mg \cdot \sin \alpha — F \cdot \cos \alpha — \mu mg \cdot \cos \alpha — \mu F \cdot \sin \alpha = 0$$

$$mg\left( {\sin \alpha — \mu \cdot \cos \alpha } \right) = F\left( {\cos \alpha + \mu \cdot \sin \alpha } \right)$$

$$F = \frac{{mg\left( {\sin \alpha — \mu \cdot \cos \alpha } \right)}}{{\cos \alpha + \mu \cdot \sin \alpha }}$$

В принципе мы решили задачу в общем виде, можно уже посчитать и численный ответ.

$$F = \frac{{3 \cdot 10 \cdot \left( {\sin 45^\circ — 0,5 \cdot \cos 45^\circ } \right)}}{{\cos 45^\circ + 0,5 \cdot \sin 45^\circ }} = 10\; Н$$

Это интересно! Если силу $F$ увеличивать, то тело также останется в покое. Вообще, при увеличении $F$ сила трения покоя сначала уменьшится до нуля, а далее сменит своё направление и будет увеличиваться. При этом её значение определяется первым законом Ньютона. Тело придет в движение, когда сила трения покоя опять примет максимальное значение. Получается, что существует целая совокупность значений силы $F$, при прикладывании которой тело будет оставаться в покое.

Получается мы можем встретить задачу, в которой спрашивается о максимальном значении силы $F$, при котором брусок будет оставаться в покое.

Ответ: 10 Н.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.3.10 С ледяной горки высотой 3 м и длиной основания 5 м съезжают санки, которые
2.3.12 Брусок сползает без начальной скорости с высоты 2 м по доске, наклоненной
2.3.13 Ледяная гора составляет с горизонтом угол 30 градусов, по ней снизу вверх пускают