Условие задачи:

Частица, начав двигаться из состояния покоя и пройдя некоторый путь равноускоренно, имела скорость 10 м/с. Какую скорость она имела, пройдя три четверти пути?

Задача №1.3.41 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\upsilon=10\) м/с, \(S_1=\frac{3}{4}S\), \(\upsilon_1-?\)

Решение задачи:

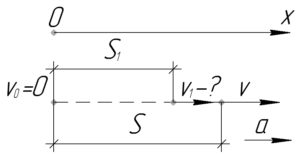Для полного пути \(S\) и для участка \(S_1\), равного \(\frac{3}{4}S\), запишем следующую известную формулу:

\[\left\{ \begin{gathered}
{\upsilon ^2} — \upsilon _0^2 = 2aS \hfill \\
\upsilon _1^2 — \upsilon _0^2 = 2a{S_1} \hfill \\
\end{gathered} \right.\]

У частицы отсутствовала начальная скорость, поэтому \(\upsilon_0=0\). Тогда система примет вид:

\[\left\{ \begin{gathered}
{\upsilon ^2} = 2aS \hfill \\
\upsilon _1^2 = 2a{S_1} \hfill \\
\end{gathered} \right.\]

Поделив нижнее уравнение на верхнее, выразим искомую скорость \(\upsilon_1\) частицы на конце участка длиной \(S_1\).

\[\frac{{\upsilon _1^2}}{{{\upsilon ^2}}} = \frac{{{S_1}}}{S} \Rightarrow \upsilon _1^2 = {\upsilon ^2}\frac{{{S_1}}}{S} \Rightarrow {\upsilon _1} = \upsilon \sqrt {\frac{{{S_1}}}{S}} \]

Так как по условию \(S_1=\frac{3}{4}S\), то:

\[{\upsilon _1} = \upsilon \sqrt {\frac{{3S}}{{4S}}}  = \frac{{\sqrt 3 }}{2}\upsilon \]

Вычислим ответ.

\[{\upsilon _1} = \frac{{\sqrt 3 }}{2} \cdot 10 = 8,66\; м/с = 31,18\; км/ч\]

Ответ: 31,18 км/ч.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

1.3.40 Точка движется равноускоренно. За 4 с она проходит путь 24 м. За следующие
1.3.42 Велосипедист начал свое движение из состояния покоя и в течение первых
1.3.43 Два велосипедиста едут навстречу: один из них, имея скорость 7,2 км/ч, спускается