icodepro.ruУсловие задачи:
Человек, стоящий на краю высохшего колодца, бросает вертикально вверх камень, сообщив ему скорость 10 м/с. Через какое время камень упадет на дно колодца, если его глубина 15 м?
Задача №1.4.31 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\upsilon_0=10\) м/с, \(H=15\) м, \(t-?\)
Решение задачи:
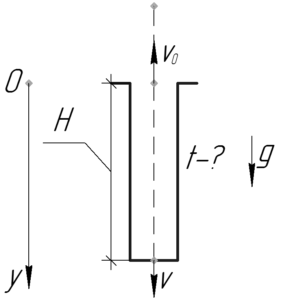Перед нами простая задача, решить которую можно, просто записав уравнение движения камня. Для этого приведем рисунок к задаче, на котором введем ось \(y\), начало которой расположим на поверхности земли. Чтобы записать вышеупомянутое уравнение, необходимо правильно спроецировать скорость и ускорение свободного падения на введенную ось \(y\). Перед слагаемым \(\upsilon_0 t\) должен быть знак «минус», так как тело бросили вверх, а ось направлена вниз. Перед слагаемым \(\frac{gt^2}{2}\) необходим знак «плюс», поскольку направление ускорения совпадает с осью \(y\). В итоге уравнение движения вдоль оси \(y\) будет выглядеть следующим образом.
\[oy:y = — {\upsilon _0}t + \frac{{g{t^2}}}{2}\]
Когда тело достигнет дна колодца, находящегося на глубине \(H\) от поверхности земли, его координата \(y\) и будет равна \(H\).
\[H = — {\upsilon _0}t + \frac{{g{t^2}}}{2}\]
Решим полученное квадратное уравнение относительно неизвестной \(t\). Подставим в уравнение численные значения величин.
\[5{t^2} — 10t — 15 = 0\]
\[{t^2} — 2t — 3 = 0\]
Заметим, что для этого квадратного уравнение \(a — b + c = 0\), где \(a,b,c\) — коэффициенты квадратного уравнения, поэтому первый корень равен -1, а второй \(-\frac{c}{a}\).
\[\left[ \begin{gathered}
t = — 1 \; с \hfill \\
t = 3 \; с \hfill \\
\end{gathered} \right.\]
Отрицательный корень не может быть ответом к задаче, поскольку отсчет времени начинается с нуля.
Ответ: 3 с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.4.30 Тело свободно падает без начальной скорости с высоты 45 м. Какой путь
1.4.32 Аэростат поднимается вертикально вверх с ускорением 2 м/с2. Через 5 с от
1.4.33 С аэростата, опускающегося со скоростью 5 м/с, бросают вертикально вверх тело
Из формулы без времени ( V^2-Vo^2=2gH) я найду высоту на которую поднялся камень от края колодца получу 5 м, сразу отсюда найдем время подъема из формулы
t1 = ?(2H/g); время спуска t2 с высоты (5 + 15) также из этой формулы;
общее время t = 1c + 2c=3c. Может кому-то проще так понять, как и мне
Решение верное, но это решение по действиям (не совсем красиво, как мне кажется).
Добавлю решение квадратного уравнения в общем виде, может быть кому-то будет интересно:\[\frac{{g{t^2}}}{2} — {\upsilon _0}t — H = 0\]\[D = \upsilon _0^2 + 2gH\]\[t = \frac{{{\upsilon _0} \pm \sqrt {\upsilon _0^2 + 2gH} }}{g}\]Корень со знаком «минус» отбрасываем, поскольку он даст отрицательное время, поэтому окончательно имеем:\[t = \frac{{{\upsilon _0} + \sqrt {\upsilon _0^2 + 2gH} }}{g}\]\[t = \frac{{10 + \sqrt {{{10}^2} + 2 \cdot 10 \cdot 15} }}{{10}} = 3\;с\]