Условие задачи:

Через раствор медного купороса пропускают ток, изменяющийся по линейному во времени закону $I=10-0,02t$ (А). Сколько меди выделится на катоде через 200 с после пропускания такого тока?

Задача №7.3.24 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$I=10-0,02t$ А, $t=200$ с, $m-?$

Решение задачи:

Для нахождения массы меди, выделившейся на катоде, необходимо использовать объединенный закон Фарадея:

$$m = \frac{1}{F}\frac{M}{n}It\;\;\;\;(1)$$

Здесь $F$ — число Фарадея, равное 96600 Кл/моль; $M$ — молярная масса меди, равная 0,064 кг/моль; $n$ — валентность меди, равная 2.

Произведение тока $I$ на время $t$ равно заряду $q$, протекшему через электролит, поэтому можем представить формулу (1) в виде:

$$m = \frac{1}{F}\frac{M}{n}q$$

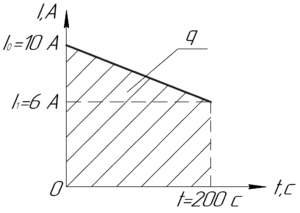
Заряд $q$ можно найти, если построить график данной в условии линейной функции. Очевидно, что начальный ток $I_0$ (то есть ток в момент времени $t=0$ с) равен 10 А, а конечный $I_1$ (то есть ток в момент времени $t=200$ с):

$$I_1 = 10 — 0,02 \cdot 200 = 6\;А$$

Если теперь построить график этой линейной функции (а мы это можем сделать, поскольку знаем координат двух точек), то заряд $q$ равен площади фигуры под графиком функции (смотрите рисунок). Эта фигура является трапецией, поэтому:

$$q = \frac{1}{2}({I_0} + {I_1})t$$

Посчитаем численное значение $q$:

$$q = \frac{1}{2} \cdot (10 + 6) \cdot 200 = 1600\;Кл$$

В итоге масса $m$ равна:

$$m = \frac{1}{{96600}} \cdot \frac{{0,064}}{2} \cdot 1600 = 5,3 \cdot {10^{ — 4}}\;кг = 0,53\;г$$

Ответ: 0,53 г.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

7.3.23 Сила тока, характеризующая поток электронов в электронно-лучевой трубке, 400 мкА
7.3.25 Определить массу меди, выделившейся из раствора медного купороса за 100 с, если сила тока
7.3.26 Электрохимический эквивалент меди 3,3×10^(-7) кг/Кл. Сколько меди выделится на электроде