icodepro.ruУсловие задачи:
Два шара, алюминиевый и цинковый, одинакового объема и радиуса 10 см скреплены в точке касания. На каком расстоянии от центра цинкового шара находится центр тяжести.
Задача №3.1.13 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(V_{Al}=V_{Zn}\), \(R=10\) см, \(l-?\)
Решение задачи:
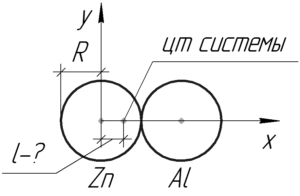Покажем на схеме два скрепленных между собой шара одинакового объема. Введем оси координат как показано на схеме. Поскольку в таком случае схема симметрична относительно оси \(x\), значит центр тяжести точно лежит на этой оси, то есть:
Координату центра тяжести системы тел \(x_{цт}\) находят по такой формуле:
\[{x_{цт}} = \frac{{\sum\limits_{i = 1}^n {{m_i}g{x_i}} }}{{\sum\limits_{i = 1}^n {{m_i}g} }}\]
Здесь \(m_{i}\) — масса i-того тела (шара), \(x_{i}\) — координата центра тяжести i-того тела (шара).
В таком случае имеем:
\[{x_{цт}} = \frac{{{m_{Al}} \cdot g \cdot 2R + {m_{Zn}} \cdot g \cdot 0}}{{{m_{Al}} \cdot g + {m_{Zn}} \cdot g}}\]
Выразим массы шаров через плотности материалов, из которых они изготовлены по известной формуле (\(m= \rho V\)).
\[{x_{цт}} = \frac{{{\rho _{Al}} \cdot V \cdot g \cdot 2R}}{{{\rho _{Al}} \cdot V \cdot g + {\rho _{Zn}} \cdot V \cdot g}}\]
\[{x_{цт}} = \frac{{{\rho _{Al}} \cdot 2R}}{{{\rho _{Al}} + {\rho _{Zn}}}}\]
Искомое расстояние \(l\) равно \(x_{цт}\):
\[l = {x_{цт}}\]
\[l = \frac{{{\rho _{Al}} \cdot 2R}}{{{\rho _{Al}} + {\rho _{Zn}}}}\]
Понятно, что 10 см = 0,1 м, плотность алюминия равна \(\rho_{Al} = 2700\; кг/м^3\), а плотность цинка — \(\rho_{Zn} = 7100\; кг/м^3\) (табличные данные). Посчитаем ответ:
\[l = \frac{{2700 \cdot 2 \cdot 0,1}}{{2700 + 7100}} = 0,0551\;м = 55,1\;мм\]
Ответ: 55,1 мм.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
3.1.12 При подвеске контактного провода троллейбусной сети провес опорного троса
3.1.14 Три однородных шара массой 1, 2 и 2 кг укреплены на легко стержне. Центр 2-ого шара
3.1.15 На одном из концов однородного стержня прикреплен груз массой 3 кг. Если стержень
А не проще ли решить через равенство моментов — МL=ml, где М и m соответственно массы цинкового и алюминиевого шаров, а L и l — соответственно, расстояния до центра масс? Тогда L=20-l, а M и m можно принять равными 7.1 кг и 2,7 кг соответственно — ведь объёмы равны и разность масс сводится к разности плотностей, тогда задача решается в 2 действия.
С уважением.
Ваше решение действительно проще, я согласен.
Я стараюсь решать задачи формально, чтобы мои рассуждения были универсальны, подошли к любой подобной задачи на определение центра тяжести.
Единственное, что я Вам советую, стараться решать задачи в общем виде, без промежуточных подстановок. Рано или поздно Вам придётся научиться так решать.
Не могу согласиться с формализованным подходом — задача должна решаться рационально, а это возможно при видении учеником физической сути задачи. А привычка подходить к решению задач формально отучает от анализа физической картины. Но это моё мнение и я его не навязываю.
С уважением.
почему 20?
Почему при нахождении х ,радиус второго тела 0.
«В таком случае имеем:
xцт=mAl·g·2R+mZn·g·0/mAl·g+mZn·g»
Это не радиусы, это координаты центра тяжести i-того тела (шара).
При введённой системе координат у алюминиевого шара эта координата будет равна 2R, а у цинкового — 0 (так как в его центре мы разместили начало отсчёта).
Спасибо