Условие задачи:

Два упругих стальных шара массами m1=0,2 кг и m2=0,1 кг подвешены рядом так, что их центры находятся на одном уровне. Первый шар отклоняют на высоту 18 см и затем отпускают. На какую высоту поднимется второй шар после упругого удара?

Задача №2.9.5 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(m_1=0,2\) кг, \(m_2=0,1\) кг, \(H=18\) см, \(h-?\)

Решение задачи:

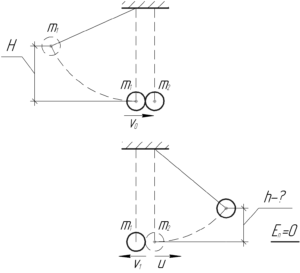Ни в какой момент движения обоих шаров потерь энергии нет, поэтому запишем законы сохранения энергии для движения первого шара до удара и второго шара после удара:

\[\left\{ \begin{gathered}
{m_1}gH = \frac{{{m_1}\upsilon _0^2}}{2} \hfill \\
\frac{{{m_2}{u^2}}}{2} = {m_2}gh \hfill \\
\end{gathered} \right.\]

Поделим нижнее равенство на верхнее, тогда:

\[\frac{h}{H} = {\left( {\frac{u}{{{\upsilon _0}}}} \right)^2}\]

\[h = H{\left( {\frac{u}{{{\upsilon _0}}}} \right)^2}\;\;\;\;(1)\]

Теперь применим закон сохранения импульса и закон сохранения энергии для моментов до и после удара:

\[\left\{ \begin{gathered}
{m_1}{\upsilon _0} = — {m_1}{\upsilon _1} + {m_2}u \;\;\;\;(2)\hfill \\
\frac{{{m_1}\upsilon _0^2}}{2} = \frac{{{m_1}\upsilon _1^2}}{2} + \frac{{{m_2}{u^2}}}{2} \;\;\;\;(3)\hfill \\
\end{gathered} \right.\]

Равенство (2) запишем в виде:

\[{m_1}\left( {{\upsilon _0} + {\upsilon _1}} \right) = {m_2}u\;\;\;\;(4)\]

В уравнении (3) перенесем в левую часть все члены с \(m_1\), вынесем его за скобки:

\[\frac{{{m_1}}}{2}\left( {\upsilon _0^2 — \upsilon _1^2} \right) = \frac{{{m_2}{u^2}}}{2}\]

Распишем разность квадратов:

\[\frac{{{m_1}}}{2}\left( {{\upsilon _0} + {\upsilon _1}} \right)\left( {{\upsilon _0} — {\upsilon _1}} \right) = \frac{{{m_2}{u^2}}}{2}\]

Учитывая (4), получим:

\[\frac{{{m_2}u}}{2}\left( {{\upsilon _0} — {\upsilon _1}} \right) = \frac{{{m_2}{u^2}}}{2}\]

\[u = {\upsilon _0} — {\upsilon _1}\;\;\;\;(5)\]

Полученное выражение для скорости второго шара подставим в (4):

\[{m_1}\left( {{\upsilon _0} + {\upsilon _1}} \right) = {m_2}\left( {{\upsilon _0} — {\upsilon _1}} \right)\]

Выполним следующие преобразования, чтобы в конечном счете выразить \(\upsilon_1\):

\[{m_1}{\upsilon _0} + {m_1}{\upsilon _1} = {m_2}{\upsilon _0} — {m_2}{\upsilon _1}\]

\[{\upsilon _1}\left( {{m_1} + {m_2}} \right) = {\upsilon _0}\left( {{m_2} — {m_1}} \right)\]

\[{\upsilon _1} = \frac{{{\upsilon _0}\left( {{m_2} — {m_1}} \right)}}{{{m_1} + {m_2}}}\]

Выразим скорость второго шарика \(u\), благодаря подстановке последнего полученного выражения в (5):

\[u = {\upsilon _0} — \frac{{{\upsilon _0}\left( {{m_2} — {m_1}} \right)}}{{{m_1} + {m_2}}} = \frac{{{\upsilon _0}\left( {{m_1} + {m_2}} \right) — {\upsilon _0}\left( {{m_2} — {m_1}} \right)}}{{{m_1} + {m_2}}}\]

\[u = \frac{{{\upsilon _0}{m_1} + {\upsilon _0}{m_2} — {\upsilon _0}{m_2} + {\upsilon _0}{m_1}}}{{{m_1} + {m_2}}}\]

\[u = \frac{{2{\upsilon _0}{m_1}}}{{{m_1} + {m_2}}}\]

Полученное подставим в (1), так мы получим решение задачи в общем виде:

\[h = H{\left( {\frac{{2{\upsilon _0}{m_1}}}{{{\upsilon _0}\left( {{m_1} + {m_2}} \right)}}} \right)^2}\]

\[h = \frac{{4m_1^2H}}{{{{\left( {{m_1} + {m_2}} \right)}^2}}}\]

Считаем численный ответ к задаче (18 см = 0,18 м):

\[h = \frac{{4 \cdot {{0,2}^2} \cdot 0,18}}{{{{\left( {0,2 + 0,1} \right)}^2}}} = 0,32\; м\]

Ответ: 0,32 м.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.9.4 Гранату бросают от поверхности земли под углом 30 градусов к горизонту
2.9.6 Шарик подлетает к неподвижной вертикальной стенке сверху со скоростью 10 м/с
2.9.7 На горизонтальной поверхности в 3 м от вертикальной стенки находится шар массой