Условие задачи:

Две бесконечные параллельные пластины равномерно заряжены поверхностной плотностью заряда 1 и -3 нКл/м². Определить напряженность поля между пластинами.

Задача №6.2.35 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$\sigma_1=1$ нКл/м², $\sigma_2=-3$ нКл/м², $E-?$

Решение задачи:

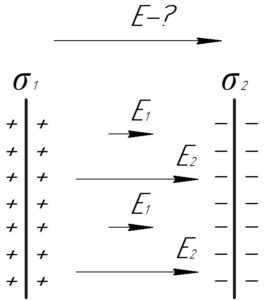Каждая из пластин будет создавать электрическое поле, направление напряженности каждого поля показано на схеме. Модуль напряженностей полей $E_1$ и $E_2$ можно найти по формулам:

$$\left\{ \begin{gathered} {E_1} = \frac{{{\sigma _1}}}{{2{\varepsilon _0}}} \hfill \\ {E_2} = \frac{{\left| {{\sigma _2}} \right|}}{{2{\varepsilon _0}}} \hfill \\ \end{gathered} \right.$$

Здесь $\varepsilon _0$ — электрическая постоянная, равная 8,85·10^-12 Ф/м.

Раскроем модуль во второй формуле (так как $\sigma_2<0$, то $\left| {{\sigma _2}} \right| = — {\sigma _2}$), тогда:

$$\left\{ \begin{gathered} {E_1} = \frac{{{\sigma _1}}}{{2{\varepsilon _0}}} \hfill \\ {E_2} = \frac{{ — {\sigma _2}}}{{2{\varepsilon _0}}} \hfill \\ \end{gathered} \right.$$

Так как напряженности $E_1$ и $E_2$ сонаправлены, то результирующее электрическое поле $E$ определим следующим образом:

$$E = {E_1} + {E_2}$$

$$E = \frac{{{\sigma _1}}}{{2{\varepsilon _0}}} — \frac{{{\sigma _2}}}{{2{\varepsilon _0}}}$$

$$E = \frac{{{\sigma _1} — {\sigma _2}}}{{2{\varepsilon _0}}}$$

Посчитаем численный ответ задачи:

$$E = \frac{{1 \cdot {{10}^{ — 9}} — \left( { — 3 \cdot {{10}^{ — 9}}} \right)}}{{2 \cdot 8,85 \cdot {{10}^{ — 12}}}} = 226\;В/м = 2,26\;В/см$$

Ответ: 2,26 В/см.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

6.2.34 Бесконечная, равномерно заряженная пластина имеет поверхностную плотность
6.2.36 Две плоские пластинки площадью 200 см2, расстояние между которыми очень мало
6.2.37 Две бесконечные плоскости, заряженные с поверхностной плотностью 2 и 0,6 мкКл/м2