Условие задачи:
Двигатель ракеты, запущенной с поверхности Земли, сообщает ей постоянное ускорение 10 м/с2, направленное вертикально вверх. Сколько времени должен проработать двигатель, чтобы ракета достигла максимальной высоты 250 м?
Задача №1.4.39 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(a=10\) м/с2, \(H=250\) м, \(t-?\)
Решение задачи:
 Неверно думать, что двигатель ракеты будет работать без остановки, постоянно придавая ей ускорение, чтобы доставить ее на высоту \(H\). Спрашиваете почему? Дело в том, что двигатель работает от ракетного топлива, и чем дольше двигатель работает, тем большую массу этого топлива он расходует, значит, тем меньшую массу полезного груза он доставит на заданную высоту.
Неверно думать, что двигатель ракеты будет работать без остановки, постоянно придавая ей ускорение, чтобы доставить ее на высоту \(H\). Спрашиваете почему? Дело в том, что двигатель работает от ракетного топлива, и чем дольше двигатель работает, тем большую массу этого топлива он расходует, значит, тем меньшую массу полезного груза он доставит на заданную высоту.
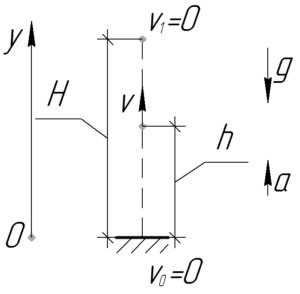
Поэтому рациональнее было бы включить двигатель на некоторое время \(t\), чтобы он достиг некоторой скорости \(\upsilon\) (и, конечно же, высоты \(h\)), чтобы затем ракета на выключенном двигателе достигла высоты \(H\), имея на этой высоте скорость \(\upsilon_1\), равную нулю. Только в этом случае мы доставим груз на нужную высоту от земли, при этом потратив наименьшее количество топлива.
В целом мы можем разделить пройденный путь на два этапа: на первом ракета разгоняется двигателем с ускорением \(a\), на втором — замедляется притяжением Земли с ускорением \(g\).
Взглянув на рисунок к задаче, можно записать следующую формулу.
\[\upsilon _1^2 — {\upsilon ^2} = — 2g\left( {H — h} \right)\]
Знак «минус» в правой части показывает, что ракета после выключения двигателя замедлялась, т.е. двигалась равнозамедленно с ускорением \(g\).
Поскольку конечная скорость ракеты \(\upsilon_1\) равна нулю, то выражение примет вид:
\[{\upsilon ^2} = 2g\left( {H — h} \right)\;\;\;\;(1)\]
Определим скорость \(\upsilon\) и высоту \(h\), на которой будет находиться ракета, в конце первого этапа по следующим известным формулам.
\[\upsilon = at\;\;\;\;(2)\]
\[h = \frac{{a{t^2}}}{2}\;\;\;\;(3)\]
Учитывать ускорение свободного падения \(g\) здесь не нужно, так как оно уже «сидит» в ускорении \(a\).
Подставим формулы (2) и (3) в формулу (1).
\[{a^2}{t^2} = 2g\left( {H — \frac{{a{t^2}}}{2}} \right)\]
Выразим из этого выражение искомое время \(t\).
\[{a^2}{t^2} = 2gH — ag{t^2}\]
\[{t^2}\left( {{a^2} + ag} \right) = 2gH\]
\[t = \sqrt {\frac{{2gH}}{{{a^2} + ag}}} \]
Подставим числа и подсчитаем долгожданный ответ на калькуляторе.
\[t = \sqrt {\frac{{2 \cdot 10 \cdot 250}}{{{{10}^2} + 10 \cdot 10}}} = 5\; с \]
Ответ: 5 с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.4.38 Вертолет поднимается вертикально вверх со скоростью 10 м/с. На высоте 50 м
1.4.40 Над шахтой глубиной 40 м вертикально вверх бросили камень со скоростью 12 м/с
1.4.41 Парашютист сразу после прыжка пролетает расстояние 50 м с пренебрежимо

 icodepro.ru
icodepro.ru
опять эта формула «из рисунка видно» ?!?
Всё гораздо проще…
высота подъёма при работающем двигателе: h = V^2/(2 a)
высота подъёма при НЕ работающем двигателе h1= V^2/(2g)
находим скорость (поскольку H = h + h1)
и следующим шагом определяем время из: V = a t