Условие задачи:
Электрон с начальной скоростью 2000 км/с, двигаясь в поле плоского конденсатора вдоль линий напряженности, полностью теряет скорость на пути 3 см. Какова разность потенциалов между обкладками, если расстояние между ними 5 см?
Задача №6.3.33 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\upsilon_0=2000\) км/с, \(\upsilon=0\) м/с, \(S=3\) см, \(d=5\) см, \(\Delta \varphi — ?\)
Решение задачи:
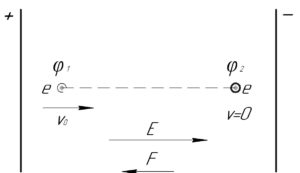 Пусть обкладки конденсатора заряжены так, как показано на схеме. Тогда чтобы электрон постепенно замедлялся при движении в конденсаторе, напряженность поля внутри конденсатора должна быть направлена слева направо, поскольку в этом случае действующая на него сила (и ускорение) будут направлены справа налево, т.е против скорости электрона.
Пусть обкладки конденсатора заряжены так, как показано на схеме. Тогда чтобы электрон постепенно замедлялся при движении в конденсаторе, напряженность поля внутри конденсатора должна быть направлена слева направо, поскольку в этом случае действующая на него сила (и ускорение) будут направлены справа налево, т.е против скорости электрона.
Поле конденсатора совершит отрицательную работу, величину которой можно найти по формуле:
\[A = — FS\]
Электрическую силу \(F\) (точнее, её модуль) легко найти из напряженности поля конденсатора \(E\) и модуля заряда электрона \(e\) (он равен 1,6·10-19 Кл) следующим образом:
\[F = Ee\]
Тогда:
\[A = — EeS \;\;\;\;(1)\]
Также работу поля можно определить как изменение кинетической энергии электрона:
\[A = \frac{{{m_e}{\upsilon ^2}}}{2} — \frac{{{m_e}\upsilon _0^2}}{2}\]
Поскольку в условии сказано, что электрон в конце полностью потеряет скорость, т.е. \(\upsilon=0\), имеем:
\[A = — \frac{{{m_e}\upsilon _0^2}}{2}\;\;\;\;(2)\]
Теперь приравняем (1) и (2) и из полученного равенства выразим напряженность поля:
\[ — EeS = — \frac{{{m_e}\upsilon _0^2}}{2}\]
\[E = \frac{{{m_e}\upsilon _0^2}}{{2eS}}\;\;\;\;(3)\]
Разность потенциалов между обкладками конденсатора \(\Delta \varphi\) и напряженность поля конденсатора связаны друг с другом соотношением:
\[E = \frac{{\Delta \varphi }}{d}\]
Значит:
\[\Delta \varphi = Ed\]
Учитывая (3), получим окончательную формулу для нахождения ответа этой задачи:
\[\Delta \varphi = \frac{{{m_e}\upsilon _0^2d}}{{2eS}}\]
Считаем ответ:
\[\Delta \varphi = \frac{{9,1 \cdot {{10}^{ — 31}} \cdot {{\left( {2000 \cdot {{10}^3}} \right)}^2} \cdot 0,05}}{{2 \cdot 1,6 \cdot {{10}^{ — 19}} \cdot 0,03}} = 18,96\;В \approx 19\;В\]
Ответ: 19 В.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.3.32 Электрон вылетает из точки, потенциал которой 600 В, со скоростью 12 Мм/с
6.3.34 В поле неподвижного точечного заряда 1 мкКл по направлению к нему движется
6.3.35 Электрическое поле в вакууме образовано точечным зарядом 1,5 нКл. На каком

 icodepro.ru
icodepro.ru