Условие задачи:
Электрон, ускоренный разностью потенциалов 1 кВ, влетает в однородное магнитное поле перпендикулярно к линиям индукции. Найти изменение импульса электрона через четверть оборота.
Задача №8.2.8 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(U=1\) кВ, \(\Delta p-?\)
Решение задачи:
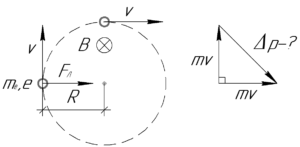 Электрон, влетевший в однородное магнитное поле перпендикулярно к линиям магнитной индукции, будет двигаться в нем равномерно по окружности. Исходя из этого понятно, что через четверть оборота импульс электрона изменится только по направлению, он станет перпендикулярным к своему начальному направлению (смотрите схему справа на рисунке). Тогда искомое изменение импульса \(\Delta p\) численно равно длине гипотенузы в указанном равнобедренном прямоугольном векторном треугольнике, поэтому (к этому можно прийти, если применить теорему Пифагора, но мы это опустим):
Электрон, влетевший в однородное магнитное поле перпендикулярно к линиям магнитной индукции, будет двигаться в нем равномерно по окружности. Исходя из этого понятно, что через четверть оборота импульс электрона изменится только по направлению, он станет перпендикулярным к своему начальному направлению (смотрите схему справа на рисунке). Тогда искомое изменение импульса \(\Delta p\) численно равно длине гипотенузы в указанном равнобедренном прямоугольном векторном треугольнике, поэтому (к этому можно прийти, если применить теорему Пифагора, но мы это опустим):
\[\Delta p = \sqrt 2 {m_e}\upsilon \;\;\;\;(1)\]
Зная, что электрон был ускорен разностью потенциалов \(U\), его скорость \(\upsilon\) можно найти по закону сохранения энергии:
\[eU = \frac{{{m_e}{\upsilon ^2}}}{2}\]
Откуда:
\[\upsilon = \sqrt {\frac{{2eU}}{{{m_e}}}} \;\;\;\;(2)\]
Подставим выражение (2) в формулу (1):
\[\Delta p = \sqrt 2 {m_e}\sqrt {\frac{{2eU}}{{{m_e}}}} \]
\[\Delta p = 2\sqrt {{m_e}eU} \]
Напомним, что масса электрона \(m_e\) равна 9,1·10-31 кг, а модуль его заряда \(e\) равен 1,6·10-19 Кл. Подставим численные данные в полученную формулу и посчитаем ответ:
\[\Delta p = 2\sqrt {9,1 \cdot {{10}^{ — 31}} \cdot 1,6 \cdot {{10}^{ — 19}} \cdot 1000} = 2,41 \cdot {10^{ — 23}}\; кг \cdot м/с\]
Ответ: 2,41·10-23 кг·м/с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
8.2.7 Во сколько раз изменится радиус траектории движения заряженной частицы в циклотроне
8.2.9 Протон описал окружность радиусом 5 см в однородном магнитном поле с индукцией 20 мТл
8.2.10 Заряженная частица движется в магнитном поле по окружности радиусом 4 см

 icodepro.ru
icodepro.ru
Так как скорость — векторная величина, то она зависит не только от модуля значения, но и от направления. Поэтому движение тела по окружности можно назвать равноускоренным. Даже если тело будет двигаться с постоянной по величине скоростью, её направление будет постоянно изменяться. Любое криволинейное движение можно свести к нескольким движениям по окружности.
Противоречивое суждение!!!
1)Так как скорость — векторная величина, то она зависит не только от модуля значения, но и от направления
2) Даже если тело будет двигаться с постоянной по величине скоростью
Упс!?!
Это как?
надо говорить:
Двигаясь по окружности с постоянной по модулю (!!!) скоростью…
и никаким боком нельзя сказать, что движение равноускоренное (при равномерном движении по окружности)
т.е. нет у автора (и ему подобных) понимания термина УСКОРЕНИЕ
Это бредовый набор слов
Так как скорость — векторная величина, то она зависит не только от модуля значения, но и от направления. Поэтому движение тела по окружности можно назвать равноускоренным. Даже если тело будет двигаться с постоянной по величине скоростью, её направление будет постоянно изменяться. Любое криволинейное движение можно свести к нескольким движениям по окружности.
Все верно, к чему Вы привели здесь этот абзац?