Условие задачи:

Есть два способа закинуть льдинку: бросить её под углом 45° к горизонту или пустить скользить по льду с коэффициентом трения о лед 0,02. Каково отношение пути льдинки при втором способе к дальности полета при первом? Сопротивлением воздуха пренебречь.

Задача №2.1.71 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\alpha=45^\circ\), \(\mu=0,02\), \(\frac{S_2}{S_1}-?\)

Решение задачи:

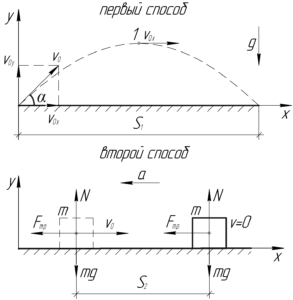При первом способе дальность полета \(S_1\) определяется по формуле:

\[{S_1} = {\upsilon _0}\cos \alpha  \cdot 2t\]

Здесь \(t\) — время движения льдинки до точки наивысшего подъема, которую можно найти из формулы скорости для равнозамедленного движения:

\[{\upsilon _y} = {\upsilon _0}\sin \alpha  — gt\]

В этой точке проекция (точка 1 на верхней схеме) скорости на ось \(y\) равна нулю, т.е. \(\upsilon _y=0\), поэтому:

\[{\upsilon _y} = 0 \Rightarrow {\upsilon _0}\sin \alpha  — gt = 0\]

\[t = \frac{{{\upsilon _0}\sin \alpha }}{g}\]

Дальность полета при первом способе равна:

\[{S_1} = \frac{{{\upsilon _0}\cos \alpha  \cdot 2{\upsilon _0}\sin \alpha }}{g} = \frac{{\upsilon _0^2\sin 2\alpha }}{g}\]

Для нахождения пути льдинки при втором способе воспользуемся теоремой об изменении кинетической энергии — работа силы трения равна по величине изменению кинетической энергии льдинки.

\[A = \Delta {W_к}\]

\[ — {F_{тр}} \cdot {S_2} = 0 — \frac{{m\upsilon _0^2}}{2}\]

\[{S_2} = \frac{{m\upsilon _0^2}}{{2{F_{тр}}}}\]

Чтобы найти силу трения, нарисуем на схеме все силы, действующие на льдинку, и применим законы Ньютона в проекции на оси:

\[\left\{ \begin{gathered}
oy:N = mg \;\;\;\;(1)\hfill \\
ox:{F_{тр}} = ma \;\;\;\;(2)\hfill \\
\end{gathered} \right.\]

Всем известно, что модуль силы трения скольжения можно найти как произведение коэффициента трения на силу нормальной реакции опоры:

\[{F_{тр}} = \mu N = \mu mg\]

Путь при втором способе можно определить из формулы:

\[{S_2} = \frac{{m\upsilon _0^2}}{{2\mu mg}} = \frac{{\upsilon _0^2}}{{2\mu g}}\]

Искомое соотношение равно:

\[\frac{{{S_2}}}{{{S_1}}} = \frac{{\upsilon _0^2 \cdot g}}{{2\mu g \cdot \upsilon _0^2\sin 2\alpha }} = \frac{1}{{2\mu \sin 2\alpha }}\]

Численно же отношение равно:

\[\frac{{{S_2}}}{{{S_1}}} = \frac{1}{{2 \cdot 0,02 \cdot \sin 90^\circ }} = 25\]

Ответ: 25.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.1.70 Два соприкасающихся бруска лежат на горизонтальном столе, по которому они могут
2.1.72 К вертикальной стенке с силой 40 Н, направленной горизонтально, прижимается брусок
2.1.73 На гладкой поверхности лежит доска массой 5 кг, на ней находится тело массой 3 кг