Условие задачи:
Гранату бросают от поверхности земли под углом 30° к горизонту с начальной скоростью 10 м/с. В верхней точке траектории граната разрывается на два одинаковых осколка, скорости которых сразу после взрыва направлены горизонтально. На каком расстоянии друг от друга упадут осколки, если кинетическая энергия, сообщенная им при взрыве, 18 Дж, а масса гранаты 1 кг?
Задача №2.9.4 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\alpha=30^\circ\), \(\upsilon_0=10\) м/с, \(m=\frac{M}{2}\) кг, \(M=1\) кг, \(E=18\) Дж, \(L-?\)
Решение задачи:
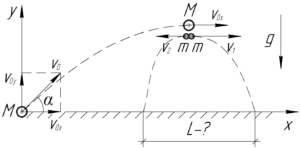 В наивысшей точке траектории граната имеет скорость \(\upsilon_0 \cos \alpha\). Учитывая это, запишем закон сохранения импульса в проекции на ось \(x\) и закон сохранения энергии для моментов до и после взрыва (смотри схему).
В наивысшей точке траектории граната имеет скорость \(\upsilon_0 \cos \alpha\). Учитывая это, запишем закон сохранения импульса в проекции на ось \(x\) и закон сохранения энергии для моментов до и после взрыва (смотри схему).
\[\left\{ \begin{gathered}
M{\upsilon _0}\cos \alpha = m{\upsilon _1} — m{\upsilon _2} \hfill \\
\frac{{M\upsilon _0^2{{\cos }^2}\alpha }}{2} + E = \frac{{m\upsilon _1^2}}{2} + \frac{{m\upsilon _2^2}}{2} \hfill \\
\end{gathered} \right.\]
Так как по условию задачи масса осколков равна \(m=\frac{M}{2}\), то:
\[\left\{ \begin{gathered}
M{\upsilon _0}\cos \alpha = \frac{M}{2}{\upsilon _1} — \frac{M}{2}{\upsilon _2} \hfill \\
\frac{{M\upsilon _0^2{{\cos }^2}\alpha }}{2} + E = \frac{{M\upsilon _1^2}}{4} + \frac{{M\upsilon _2^2}}{4} \hfill \\
\end{gathered} \right.\]
\[\left\{ \begin{gathered}
2{\upsilon _0}\cos \alpha = {\upsilon _1} — {\upsilon _2} \;\;\;\;(1)\hfill \\
\frac{{M\upsilon _0^2{{\cos }^2}\alpha }}{2} + E = \frac{M}{4}\left( {\upsilon _1^2 + \upsilon _2^2} \right) \;\;\;\;(2)\hfill \\
\end{gathered} \right.\]
Мы получили два равенства. Из равенства (2) выразим сумму квадратов скоростей осколков:
\[\upsilon _1^2 + \upsilon _2^2 = \frac{4}{M}\left( {\frac{{M\upsilon _0^2{{\cos }^2}\alpha }}{2} + E} \right)\;\;\;\;(3)\]
А вот обе части равенства (1) системы возведем в квадрат, чтобы найти удвоенное произведение скоростей осколков:
\[4\upsilon _0^2{\cos ^2}\alpha = \upsilon _1^2 — 2{\upsilon _1}{\upsilon _2} + \upsilon _2^2\]
\[2{\upsilon _1}{\upsilon _2} = \upsilon _1^2 + \upsilon _2^2 — 4\upsilon _0^2{\cos ^2}\alpha \]
Учитывая (3), последнее выражение примет вид:
\[2{\upsilon _1}{\upsilon _2} = \frac{4}{M}\left( {\frac{{M\upsilon _0^2{{\cos }^2}\alpha }}{2} + E} \right) — 4\upsilon _0^2{\cos ^2}\alpha \;\;\;\;(4)\]
Думаю, вам сейчас совсем непонятно, зачем мы все это делали, но вскоре вы все поймете.
Искомое расстояние между упавшими осколками \(L\), очевидно, равно:
\[L = \left( {{\upsilon _1} + {\upsilon _2}} \right)t\]
Здесь \(t\) — время падения осколков, оно равно времени подъема гранаты до наивысшей точки траектории:
\[t = \frac{{{\upsilon _0}\sin \alpha }}{g}\]
Тогда:
\[L = \left( {{\upsilon _1} + {\upsilon _2}} \right)\frac{{{\upsilon _0}\sin \alpha }}{g}\]
Внимание! Делаю хитрость, возвожу в квадрат обе части, тогда:
\[{L^2} = {\left( {{\upsilon _1} + {\upsilon _2}} \right)^2}\frac{{\upsilon _0^2{{\sin }^2}\alpha }}{{{g^2}}}\]
Раскрою квадрат суммы в правой части. Тогда искомое расстояние равно:
\[L = \frac{{{\upsilon _0}\sin \alpha }}{g}\sqrt {\upsilon _1^2 + 2{\upsilon _1}{\upsilon _2} + \upsilon _2^2} \]
Ранее мы уже нашли сумму квадратов (3) и удвоенное произведение (4), в итоге:
\[L = \frac{{{\upsilon _0}\sin \alpha }}{g}\sqrt {\frac{8}{M}\left( {\frac{{M\upsilon _0^2{{\cos }^2}\alpha }}{2} + E} \right) — 4\upsilon _0^2{{\cos }^2}\alpha } \]
\[L = \frac{{{\upsilon _0}\sin \alpha }}{g}\sqrt {4\upsilon _0^2{{\cos }^2}\alpha + \frac{{8E}}{M} — 4\upsilon _0^2{{\cos }^2}\alpha } \]
\[L = \frac{{{\upsilon _0}\sin \alpha }}{g}\sqrt {\frac{{8E}}{M}} \]
После всех «ужасных» преобразований, мы получили «красивый» ответ. Подставляем данные задачи в формулу и считаем ответ:
\[L = \frac{{10 \cdot \sin 30^\circ }}{{10}}\sqrt {\frac{{8 \cdot 18}}{1}} = 6\; м\]
Ответ: 6 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.9.3 Во сколько раз уменьшится энергия нейтрона n при столкновении с ядром углерода C
2.9.5 Два упругих стальных шара массами m1=0,2 кг и m2=0,1 кг подвешены рядом
2.9.6 Шарик подлетает к неподвижной вертикальной стенке сверху со скоростью 10 м/с

 icodepro.ru
icodepro.ru
Здравствуйте, а почему в законе сохранения энергии стоит проекция скорости?
Технически — это полная скорость в момент взрыва гранаты. Но замечу, что она равна проекции начальной скорости на ось x.
Здравствуйте, почему время падения осколка равно v0*sin?/g?
за конечную координату по оси y принимаем 0, тогда уравнение координаты имеет вид:
0=v0*t*sin(a) — gt2/2, следовательно уравнение времени(t)=2v0*sin(a)/g
Куда делась двойка?
Вы нашли общее время полёта гранаты (а не осколков) до падения на землю, то есть если бы она не разорвалась в верхней точке.
Половину этого времени, т.е. t=v0*sin(a)/g, граната летит до верхней точки. Там она взрывается. Далее осколки летят вниз то же время, поскольку скорости осколков после взрыва направлены горизонтально. Иначе говоря, взрыв не изменил вертикальной составляющей скорости гранаты (и осколков), именно поэтому они будут лететь вниз в течение времени, равное t=v0*sin(a)/g.