icodepro.ruУсловие задачи:
Хоккейная шайба, имея начальную скорость 5 м/с, скользит до удара о борт площадки 10 м. Удар считать абсолютно упругим, коэффициент трения шайбы о лед 0,1, сопротивлением воздуха пренебречь. Какой путь пройдет шайба после удара?
Задача №2.1.69 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\upsilon_0=5\) м/с, \(S_1=10\) м, \(\mu=0,1\), \(S_2-?\)
Решение задачи:
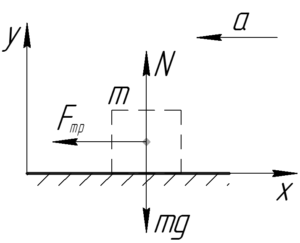Так как удар был абсолютно упругим, то потерь скорости шайбы при ударе не было, а значит и не было потерь кинетической энергии. Применим теорему об изменении кинетической энергии. Суть её в том, что работа некоторой силы вызывает изменение кинетической энергии тела:
\[A = \Delta {W_к}\;\;\;\;(1)\]
Работу совершает только сила трения. Она равна:
\[A = — F_{тр}\left( {{S_1} + {S_2}} \right)\;\;\;\;(2)\]
Обратите внимание, что работа силы трения есть произведение силы на путь, а не перемещение. Это вызвано тем, что сила трения является неконсервативной силой.
Скорость шайбы из-за трения о лед рано или поздно упадет до нуля, поэтому изменение кинетической энергии, очевидно, равно:
\[\Delta {W_к} = 0 — \frac{{m\upsilon _0^2}}{2}\;\;\;\;(3)\]
Найдем проекции сил, действующих на тело, и запишем законы Ньютона:
\[\left\{ \begin{gathered}
oy:N = mg \hfill \\
ox:{F_{тр}} = ma \hfill \\
\end{gathered} \right.\]
Силу трения скольжения определим по формуле:
\[{F_{тр}} = \mu N = \mu mg\;\;\;\;(4)\]
Подставим (4) в (2), а полученное вместе с (3) в (1).
\[ — \mu mg\left( {{S_1} + {S_2}} \right) = 0 — \frac{{m\upsilon _0^2}}{2}\]
\[\mu g\left( {{S_1} + {S_2}} \right) = \frac{{\upsilon _0^2}}{2}\]
\[{S_2} = \frac{{\upsilon _0^2}}{{2\mu g}} — {S_1}\]
Посчитаем ответ:
\[{S_2} = \frac{{{5^2}}}{{2 \cdot 0,1 \cdot 10}} — 10 = 2,5\; м\]
Ответ: 2,5 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.1.68 Что покажут пружинные весы в лифте при измерении веса груза массой 1 кг
2.1.70 Два соприкасающихся бруска лежат на горизонтальном столе, по которому они могут
2.1.71 Есть два способа закинуть льдинку: бросить её под углом 45 градусов к горизонту или
Спасибо
Почему не mV02/2 — FтрS= mV2/2 ( найдем V — скорость с которой шайба летит обратно)
mV2/2 — FтрS= mgS (выражаем S)
Скорее вот так:
\[\left\{ \begin{gathered}
\frac{{m\upsilon _0^2}}{2} — {F_{тр}}{S_1} = \frac{{m{\upsilon ^2}}}{2} \hfill \\
\frac{{m{\upsilon ^2}}}{2} — {F_{тр}}{S_2} = 0 \hfill \\
\end{gathered} \right.\]
Откуда у Вас взялось \(mgS\) мне не понятно, сила тяжести же работу не совершает.
С mgS согласна, но по вашей системе ответ тоже не получается
Почему не получится? Из второго уравнения имеем:
\[\frac{{m{\upsilon ^2}}}{2} = {F_{тр}}{S_2}\]
Полученное подставляем в первое уравнение:
\[\frac{{m\upsilon _0^2}}{2} — {F_{тр}}{S_1} = {F_{тр}}{S_2}\]
\[\frac{{m\upsilon _0^2}}{2} = {F_{тр}}{S_1} + {F_{тр}}{S_2}\]
\[\frac{{m\upsilon _0^2}}{2} = {F_{тр}}\left( {{S_1} + {S_2}} \right)\]
Дальше всё как в решении, приведенном выше