Условие задачи:
Искусственный спутник Земли движется на высоте 12800 км. Найти скорость движения спутника.
Задача №2.5.4 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(H=12800\) км, \(\upsilon-?\)
Решение задачи:
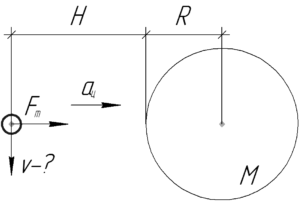 При движении спутника вокруг Земли по круговой орбите сила тяготения \(F_т\) сообщает ему центростремительное ускорение, поэтому второй закон Ньютона запишется в следующем виде:
При движении спутника вокруг Земли по круговой орбите сила тяготения \(F_т\) сообщает ему центростремительное ускорение, поэтому второй закон Ньютона запишется в следующем виде:
\[{F_т} = m{a_ц}\;\;\;\;(1)\]
Силу тяготения определяют по закону всемирного тяготения:
\[{F_т} = G\frac{{Mm}}{{{{\left( {R + H} \right)}^2}}}\;\;\;\;(2)\]
Если спутник движется с некоторой скоростью \(\upsilon\), то центростремительное ускорение равно:
\[{a_ц} = \frac{{{\upsilon ^2}}}{{R + H}}\;\;\;\;(3)\]
Подставим выражения (2) и (3) в равенство (1), тогда:
\[G\frac{{Mm}}{{{{\left( {R + H} \right)}^2}}} = \frac{{m{\upsilon ^2}}}{{R + H}}\]
Путем простых математических действий получим такое выражение для определения скорости спутника \(\upsilon\):
\[\upsilon = \sqrt {G\frac{M}{{R + H}}} \]
Можно считать ответ по этой формуле, но мы сделаем следующий трюк — дробь под корнем домножим и поделим на \(R^2\) (это можно делать благодаря основному свойству дроби), тогда:
\[\upsilon = \sqrt {G\frac{M}{{{R^2}}}\frac{{{R^2}}}{{R + H}}} \]
Заметим, то выражение \({G\frac{M}{{{R^2}}}}\) равно ускорению свободного падения \(g\) вблизи поверхности Земли (\(g=10\) м/с2). Значит:
\[\upsilon = \sqrt {\frac{{g{R^2}}}{{R + H}}} \]
\[\upsilon = R\sqrt {\frac{g}{{R + H}}} \]
Переведем высоту орбиты спутника в систему СИ:
\[12800\; км = 12,8 \cdot {10^6}\; м\]
Посчитаем численный ответ (напомним, что радиус Земли — это табличная величина, равная 6,4·106 м):
\[\upsilon = 6,4 \cdot {10^6} \cdot \sqrt {\frac{{9,8}}{{6,4 \cdot {{10}^6} + 12,8 \cdot {{10}^6}}}} = 4618,8\; м/с \approx 4,62\; км/с\]
Ответ: 4,62 км/с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.5.3 Во сколько раз ускорение свободного падения около поверхности Земли больше
2.5.5 Каково ускорение свободного падения на поверхности Солнца, если радиус Солнца
2.5.6 На какое расстояние от поверхности Земли нужно удалить тело, чтобы сила тяготения

 icodepro.ru
icodepro.ru
Переведем высоту орбиты спутника в систему СИ 12,8*10^6 метров
Исправил, спасибо за замечание!