Условие задачи:

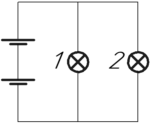К полюсам батареи из двух источников, каждый с ЭДС 75 В и внутренним сопротивлением 4 Ом, подведены две медные шины сопротивлением 10 Ом каждая. К концам шин и к их серединам подключены две лампочки сопротивлением 20 Ом каждая. Сопротивлением подводящих проводов пренебречь. Чему равен ток во второй лампочке?

Задача №7.2.47 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\rm E=75\) В, \(r=4\) Ом, \(R_1=10\) Ом, \(R_2=20\) Ом, \(I_2-?\)

Решение задачи:

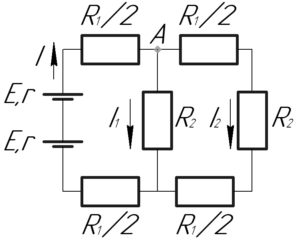Если посмотреть на схему, то в принципе понятно, что в узле A ток \(I\) разделяется на два тока: ток \(I_1\) и ток \(I_2\), поэтому верно (строго говоря, это первый закон Кирхгофа):

\[I = {I_1} + {I_2}\;\;\;\;(1)\]

Так как сопротивления \(R_2\) и \(\left( {{R_1} + {R_2}} \right)\) соединены параллельно (то есть напряжения на них одинаковы), то справедливо равенство:

\[{I_1}{R_2} = {I_2}\left( {{R_1} + {R_2}} \right)\]

Выразим из этого равенства ток \(I_1\):

\[{I_1} = \frac{{{I_2}\left( {{R_1} + {R_2}} \right)}}{{{R_2}}}\]

Полученное подставим в (1), тогда:

\[I = \frac{{{I_2}\left( {{R_1} + {R_2}} \right)}}{{{R_2}}} + {I_2}\]

\[I = \frac{{{I_2}\left( {{R_1} + 2{R_2}} \right)}}{{{R_2}}}\]

Отсюда выразим искомый ток \(I_2\):

\[{I_2} = \frac{{I{R_2}}}{{{R_1} + 2{R_2}}}\;\;\;\;(2)\]

Чтобы узнать ток \(I\), запишем закон Ома для полной цепи (учитывая, что батарея составлена из двух одинаковых последовательно соединенных ЭДС):

\[I = \frac{{2{\rm E}}}{{R + 2r}}\;\;\;\;(3)\]

Здесь \(R\) — внешнее сопротивление цепи, которое можно найти по формуле (как эквивалентное сопротивление параллельно соединенных резисторов \(R_2\) и \(\left( {{R_1} + {R_2}} \right)\), которые соединены последовательно с двумя резисторами \(\frac{R_1}{2}\)):

\[R = {R_1} + \frac{{{R_2}\left( {{R_1} + {R_2}} \right)}}{{{R_1} + 2{R_2}}}\;\;\;\;(4)\]

Смысла решать задачу в общем виде нет (так как мы просто получим гигантскую формулу), поэтому сначала найдем сопротивление внешней цепи \(R\) по формуле (4), далее найдем ток \(I\) в цепи по формуле (3), а потом уже посчитаем искомый ток во втором сопротивлении \(I_2\) по формуле (2).

\[R = 10 + \frac{{20 \cdot \left( {10 + 20} \right)}}{{10 + 2 \cdot 20}} = 22\;Ом\]

\[I = \frac{{2 \cdot 75}}{{22 + 2 \cdot 4}} = 5\;А\]

\[{I_2} = \frac{{5 \cdot 20}}{{10 + 2 \cdot 20}} = 2\;А\]

Ответ: 2 А.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

7.2.46 В указанной электрической схеме R1=R2=R3=6 Ом, ЭДС источника тока E=3,9 В, а его внутреннее
7.3.1 Через некоторое сечение электролитической ванны положительные ионы перенесли за 1 с
7.3.2 В газе между двумя электродами образуется 2×10^18 ионов в секунду. Найти силу тока в газе