Условие задачи:
Какое расстояние по горизонтали до первого удара о пол пролетит мяч, брошенный со скоростью 10 м/с под углом 60° к горизонту, если он упруго ударится о потолок высотой 3 м?
Задача №1.6.18 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(v_0=10\) м/с, \(\alpha=60^\circ\), \(H=3\) м, \(L-?\)
Решение задачи:
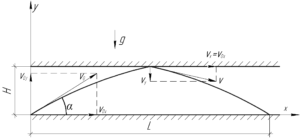 Рисунок к задаче изображен справа, для его увеличения кликните по нему мышью. Найдем время полета мяча до столкновения с потолком, для чего запишем уравнения движения мяча в проекциях на оси \(x\) и \(y\).
Рисунок к задаче изображен справа, для его увеличения кликните по нему мышью. Найдем время полета мяча до столкновения с потолком, для чего запишем уравнения движения мяча в проекциях на оси \(x\) и \(y\).
\[\left\{ \begin{gathered}
ox:x = {v_0}\cos \alpha \cdot t\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1) \hfill \\
oy:y = {v_0}\sin \alpha \cdot t — \frac{{g{t^2}}}{2}\,\,\,(2) \hfill \\
\end{gathered} \right.\]
Т.к. до столкновения с потолком мяча пройдет по вертикали высоту \(H=3\) м, то можно найти время из уравнения (2).
\[H = {v_0}\sin \alpha \cdot t — \frac{{g{t^2}}}{2}\]
\[g{t^2} — 2{v_0}\sin \alpha \cdot t + 2H = 0\]
Решим данное квадратное уравнение:
\[D = 4v_0^2{\sin ^2}\alpha — 8gH\]
\[t = \frac{{2{v_0}\sin \alpha \pm \sqrt {4v_0^2{{\sin }^2}\alpha — 8gH} }}{{2g}}\]
Подставим исходные данные для получения численного ответа:
\[t = \frac{{2 \cdot 10 \cdot \sin 60^\circ \pm \sqrt {4 \cdot {{10}^2} \cdot {{\sin }^2}60^\circ — 8 \cdot 10 \cdot 3} }}{{2 \cdot 10}}\]
\[\left[ \begin{gathered}
t = 1,25 \;с\hfill \\
t = 0,48 \;с\hfill \\
\end{gathered} \right.\]
Получили два корня, но какой из них показывает время полета? Ответ на этот вопрос — второй корень, меньший из них. Первый же показывает время полета, когда мяч находился бы на этой высоте второй раз, если бы потолка не было.
После удара о потолок мяч будет двигать до удара о пол такое же время, поэтому по горизонтали мяч пройдет расстояние:
\[L = 2{v_0}\cos \alpha \cdot t\]
Подставим исходные данные и получим ответ:
\[L = 2 \cdot 10 \cdot \cos 60^\circ \cdot 0,48 = 4,8\; м.\]
Ответ: 4,8 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Если Вам понравилась задача и ее решение, то Вы можете поделитесь ею с друзьями с помощью этих кнопок.
Смотрите также задачи:
1.6.17 Из шланга, лежащего на земле, бьет под углом 45° к горизонту вода
1.6.19 Какой скоростью обладал мальчик при прыжке с трамплина
1.6.20 С вершины холма бросают камень с начальной скоростью

 icodepro.ru
icodepro.ru
Почему после удара о потолок мяч будет двигать до удара о пол такое же время
По закону сохранения энергии скорость мяча при броске и при приземлении будут равны, поскольку потерь энергии нигде нет. Запишем формулу скорости для равноускоренного движения (в общем случае, НЕприменительно к этой задаче): \[t = \frac{{\upsilon — {\upsilon _0}}}{a}\] Отсюда видно, что если скорости для движения вверх и вниз равны (по модулю), то и время будет одинаковым.
Благодарю
t = 1,5 c
t = 0,23 c
У меня получились другие корни уравнения, попробуйте пересчитать
Куда делась вертикальная составляющая скорости после удара, ведь она не равна 0 в момент удара, тогда время полета до земли после взаимодействия будет существенно меньше, чем время подъёма?
Прошу прощения, проверив, выяснилось, что время подъёма и падения всё-таки совпадают, а вот Vx в начале движения и непосредственно перед ударом не совпадают, 2 раза одно и то же получается
Каким образом вертикальная составляющих \(\upsilon_x\) могла измениться, если по горизонтали на мяч не действуют никакие силы, а удар является упругим?
Почему скорость после удара о потолок, такая же как и начальная, ведь на мяч действует сила тяжести?
С чего Вы это взяли, в решении об этом не говорится (на схеме эти скорости различны — v_0 и v)