Условие задачи:
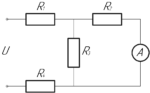 Какой ток покажет амперметр, если напряжение \(U=15\) В, сопротивления \(R_1=5\) Ом, \(R_2=10\) Ом, \(R_3=10\) Ом и \(R_4=5\) Ом. Внутренним сопротивлением амперметра пренебречь.
Какой ток покажет амперметр, если напряжение \(U=15\) В, сопротивления \(R_1=5\) Ом, \(R_2=10\) Ом, \(R_3=10\) Ом и \(R_4=5\) Ом. Внутренним сопротивлением амперметра пренебречь.
Задача №7.1.27 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(U=15\) В, \(R_1=5\) Ом, \(R_2=10\) Ом, \(R_3=10\) Ом, \(R_4=5\) Ом, \(I_2-?\)
Решение задачи:
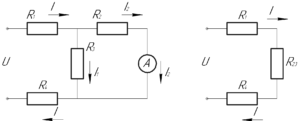 Если посмотреть на представленную схему, то можно заметить, что амперметр (сопротивление которого пренебрежимо мало) и резистор \(R_2\) соединены с резистором \(R_3\) параллельно, значит на резисторах наблюдается одинаковое напряжение. Запишем для них следствие из закона Ома для участка цепи:
Если посмотреть на представленную схему, то можно заметить, что амперметр (сопротивление которого пренебрежимо мало) и резистор \(R_2\) соединены с резистором \(R_3\) параллельно, значит на резисторах наблюдается одинаковое напряжение. Запишем для них следствие из закона Ома для участка цепи:
\[\left\{ \begin{gathered}
U = {I_2}{R_2} \hfill \\
U = {I_3}{R_3} \hfill \\
\end{gathered} \right.\]
То есть:
\[{I_2}{R_2} = {I_3}{R_3}\]
\[{I_2} = {I_3}\frac{{{R_3}}}{{{R_2}}}\]
По условию этой задачи \(R_2=10\) Ом и \(R_3=10\) Ом, то есть они одинаковы, поэтому:
\[{I_2} = {I_3}\]
Получается, что ток \(I\), протекающий через сопротивление \(R_1\), равен сумме одинаковых токов \(I_2\) и \(I_3\), поэтому верно:
\[{I_2} = \frac{I}{2}\;\;\;\;(1)\]
Чтобы найти ток \(I\), нужно определить общее сопротивление цепи \(R\). Так как сопротивления \(R_2\) и \(R_3\), как уже было сказано, соединены параллельно, а внутренним сопротивление амперметра можно пренебречь, то их эквивалентное сопротивление \(R_{23}\) равно:
\[{R_{23}} = \frac{{{R_2} \cdot {R_3}}}{{{R_2} + {R_3}}}\]
Так как \(R_2 = R_3\), то:
\[{R_{23}} = \frac{{{R_2}}}{2}\;\;\;\;(2)\]
Получается, что вся электрическая цепь состоит из трех последовательно соединенных сопротивлений \(R_1\), \(R_{23}\) и \(R_4\), поэтому общее сопротивление \(R\) равно:
\[R = {R_1} + {R_{23}} + {R_4}\]
Учитывая (2), имеем:
\[R = {R_1} + \frac{{{R_2}}}{2} + {R_4}\]
\[R = \frac{{2{R_1} + {R_2} + 2{R_4}}}{2}\;\;\;\;(3)\]
Тогда согласно закону Ома сила тока \(I\) равна:
\[I = \frac{U}{R}\]
Подставим в эту формулу выражение (3):
\[I = \frac{{2U}}{{2{R_1} + {R_2} + 2{R_4}}}\]
Принимая во внимание (1), окончательный ответ выглядит так:
\[{I_2} = \frac{{U}}{{2{R_1} + {R_2} + 2{R_4}}}\]
\[{I_2} = \frac{{15}}{{2 \cdot 5 + 10 + 2 \cdot 5}} = 0,5\;А = 500\;мА\]
Ответ: 500 мА.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
7.1.26 К концам медного провода длиной 200 м приложено напряжение 18 В. Определить среднюю
7.1.28 За одну минуту через поперечное сечение проводника прошел заряд 180 Кл
7.1.29 Какой ток покажет амперметр, если R1=1,25 Ом, R2=1 Ом, R3=3 Ом, R4=7 Ом, напряжение

 icodepro.ru
icodepro.ru
Вы потеряли двойку в последнем действии, где подставляли числа