Условие задачи:
Каков коэффициент жесткости буксировочного троса, если при буксировке автомобиля массой 2 т трос удлинился на 0,01 м, причем автомобиль через 4 с после начала движения достиг скорости 2 м/с. Трением пренебречь. Движение считать равноускоренным.
Задача №2.6.7 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m=2\) т, \(x=0,01\) м, \(t=4\) с, \(\upsilon=2\) м/с, \(k-?\)
Решение задачи:
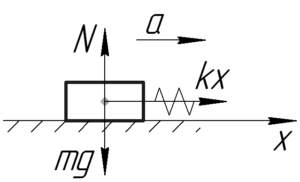 На автомобиль вдоль оси \(x\) действует только сила упругости, поэтому второй закон Ньютона в проекции на эту ось запишется в следующем виде:
На автомобиль вдоль оси \(x\) действует только сила упругости, поэтому второй закон Ньютона в проекции на эту ось запишется в следующем виде:
\[kx = ma\]
Запишем также формулу определения ускорения:
\[a = \frac{{\upsilon — {\upsilon _0}}}{t}\]
Так как начальная скорость автомобиля \(\upsilon_0\) равна нулю, то:
\[a = \frac{\upsilon }{t}\]
Самое первое равенство в таком случае примет такой вид:
\[kx = m\frac{\upsilon }{t}\]
\[k = \frac{{m\upsilon }}{{xt}}\]
Переведем массу машины в систему СИ и посчитаем ответ.
\[2\; т = 2000\; кг\]
\[k = \frac{{2000 \cdot 2}}{{0,01 \cdot 4}} = {10^5}\; Н/м = 100\; кН/м\]
Ответ: 100 кН/м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.6.6 Груз массой 1 кг, прикрепленный к пружине, равномерно тянут по горизонтальной
2.6.8 Найти удлинение буксирного троса с жесткостью 100 кН/м при буксировке автомобиля
2.6.9 Тело массой 2 кг тянут по гладкой горизонтальной поверхности с помощью пружины

 icodepro.ru
icodepro.ru