Условие задачи:

Какую работу необходимо совершить, чтобы три одинаковых точечных положительных заряда \(q\), находящихся в вакууме вдоль одной прямой на расстоянии \(a\) друг от друга, расположить в вершинах равностороннего треугольника со стороной \(a/2\)?

Задача №6.3.61 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(q\), \(a\), \(a/2\), \(A-?\)

Решение задачи:

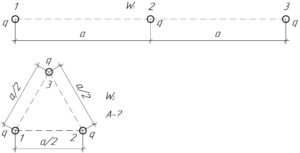Известно, что работу можно найти как изменение полной энергии системы из трёх точечных зарядов. Поскольку эти три заряда в начале и в конце будут покоиться (то есть не будут иметь скорости, а значит и кинетической энергии), то нахождение искомой работы \(A\) сводится к нахождению изменения потенциальной энергии системы \(\Delta {W_п}\) из трёх зарядов.

\[A = \Delta {W_п}\]

\[A = {W_2} — {W_1}\;\;\;\;(1)\]

В общем случае потенциальную энергию взаимодействия пары зарядов можно найти по формуле:

\[W = \frac{{k{q_1}{q_2}}}{l}\]

Здесь \(k\) — коэффициент пропорциональности, равный 9·10⁹ Н·м²/Кл², \(q_1\) и \(q_2\) — величины зарядов, \(l\) — расстояние между зарядами. Если зарядов несколько, то нужно сложить потенциальные энергии всех пар зарядов. Например, в случае трёх зарядов таких пар будет три.

Потенциальную энергию \(W_2\) взаимодействия трёх зарядов \(q\), находящихся в вершинах равностороннего треугольника со стороной \(a/2\), можно найти по такой формуле, поскольку в данном случае имеются три пары зарядов \(q\), находящихся на расстоянии \(a/2\) друг от друга:

\[{W_2} = 3 \cdot \frac{{k{q^2}}}{{\frac{a}{2}}} = \frac{{6k{q^2}}}{a}\;\;\;\;(2)\]

В случае трёх одинаковых точечных положительных зарядов \(q\), находящихся в вакууме вдоль одной прямой на расстоянии \(a\) друг от друга, будем иметь две пары зарядов \(q\), находящихся на расстоянии \(a\) друг от друга (1-2 и 2-3 на рисунке), и одну пару зарядов \(q\), находящихся на расстоянии \(2a\) (пара 1-3 на рисунке). Поэтому потенциальную энергию \(W_1\) следует искать по формуле:

\[{W_1} = 2 \cdot \frac{{k{q^2}}}{a} + \frac{{k{q^2}}}{{2a}} = \frac{{5k{q^2}}}{{2a}}\;\;\;\;(3)\]

Подставим (2) и (3) в (1), тогда получим:

\[A = \frac{{6k{q^2}}}{a} — \frac{{5k{q^2}}}{{2a}}\]

\[A = \frac{{7k{q^2}}}{{2a}}\]

Учитывая то, что \(k = \frac{1}{{4\pi {\varepsilon _0}}}\), окончательно имеем:

\[A = \frac{{7{q^2}}}{{8\pi {\varepsilon _0}a}}\]

Ответ: \(\frac{{7{q^2}}}{{8\pi {\varepsilon _0}a}}\).

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

6.3.60 По тонкому проволочному кольцу радиуса 3 см равномерно распределен заряд 10^(-9) Кл
6.3.62 В центре закрепленной полусферы радиуса R, заряженной равномерно с поверхностной
6.3.63 В центре закрепленной полусферы радиуса R, заряженной равномерно