Условие задачи:

Камень брошен вертикально вниз со скоростью \(\upsilon_0=5\) м/с. Определить среднюю скорость перемещения за первые 5 с.

Задача №1.4.10 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\upsilon_0=5\) м/с, \(t=5\) с, \(\upsilon_{ср}-?\)

Решение задачи:

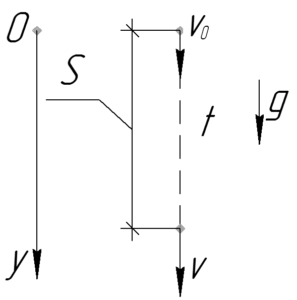Среднюю скорость можно найти, поделив пройденный путь \(S\) на затраченное время \(t\).

\[{\upsilon _{ср}} = \frac{S}{t}\;\;\;\;(1)\]

Значит осталось лишь определить, сколько пройдет камень за 5 секунд. Для этого запишем уравнение движения вдоль оси \(y\).

\[oy:y = {\upsilon _0}t + \frac{{g{t^2}}}{2}\]

Координата тела \(y\) в момент времени 5 секунд и будет являться пройденным путем \(S\).

\[S = {\upsilon _0}t + \frac{{g{t^2}}}{2}\;\;\;\;(2)\]

Подставим полученное выражение (2) в формулу средней скорости (1).

\[{\upsilon _{ср}} = \frac{{{\upsilon _0}t + \frac{{g{t^2}}}{2}}}{t}\]

Поделив почленно числитель на знаменатель, получим:

\[{\upsilon _{ср}} = {\upsilon _0} + \frac{{gt}}{2}\]

Теперь мы видим, что средняя скорость тела, падающего вертикально вниз, возрастает со временем.

Подставив численные данные сосчитаем ответ в задаче.

\[{\upsilon _{ср}} = 5 + \frac{{10 \cdot 5}}{2} = 30\; м/с = 108\; км/ч \]

Ответ: 108 км/ч.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

1.4.9 Тело брошено со скоростью 40 м/с. Определить высоту подъема тела
1.4.11 Камень, брошенный вертикально вверх со скоростью 12 м/с, через 1 с
1.4.12 Мяч брошен вверх со скоростью 10 м/с. На каком расстоянии от поверхности