Условие задачи:
Камень, брошенный горизонтально с обрыва высотой 10 м, упал на расстоянии 14 м от точки бросания. Определить начальную скорость.
Задача №1.5.7 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(H=10\) м, \(S=14\) м, \(\upsilon_0-?\)
Решение задачи:
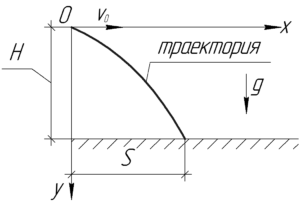 Изобразим на рисунке точку бросания камня, проведем из нее горизонтальную ось \(x\) и вертикальную ось \(y\), направленную к земле. Покажем параболическую траекторию полета и расстояния \(H\) и \(S\), пройденные телом по вертикали и горизонтали соответственно.
Изобразим на рисунке точку бросания камня, проведем из нее горизонтальную ось \(x\) и вертикальную ось \(y\), направленную к земле. Покажем параболическую траекторию полета и расстояния \(H\) и \(S\), пройденные телом по вертикали и горизонтали соответственно.
Запишем уравнения движения камня в проекциях на ось \(x\) и \(y\).
\[\left\{ \begin{gathered}
ox:x = {\upsilon _0}t\,\,\,\,\,\,(1) \hfill \\
oy:y = \frac{{g{t^2}}}{2}\,\,\,(2) \hfill \\
\end{gathered} \right.\]
Если принять за \(t\) — полное время падения, то справедливо:
\[\left\{ \begin{gathered}
S = {\upsilon _0}t\,\,\,\,\,\,(3) \hfill \\
H = \frac{{g{t^2}}}{2}\,\,\,(4) \hfill \\
\end{gathered} \right.\]
Выразим из формулы (3) искомую начальную скорость \(\upsilon_0\), а из формулы (4) найдем полное время падения \(t\).
\[S = {\upsilon _0}t \Rightarrow {\upsilon _0} = \frac{S}{t}\,\,\,(5) \]
\[H = \frac{{g{t^2}}}{2} \Rightarrow t = \sqrt {\frac{{2H}}{g}}\,\,\,(6) \]
Подставив (6) в (5), в итоге получим окончательную формулу для расчета ответа.
\[{\upsilon _0} = S\sqrt {\frac{g}{{2H}}} \]
\[{\upsilon _0} = 14\sqrt {\frac{{10}}{{2 \cdot 10}}} = 9,9 \; м/с \approx 36\; км/ч \]
Ответ: 36 км/ч.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.5.6 Камень, брошенный горизонтально с вышки, через 3 с упал на землю
1.5.8 Понижение траектории снаряда, выпущенного из горизонтально расположенного
1.5.9 Тело брошено с высоты 2 м горизонтально так, что к поверхности земли

 icodepro.ru
icodepro.ru
а зачем переворачивать дробь под корнем?
Поскольку мы подставляем дробь \(\sqrt {\frac{{2H}}{g}} \) (далее — первая дробь) в знаменатель второй дроби вместо \(t\), то фактически это означает, что мы числитель второй дроби должны умножить на перевернутую первую дробь. Почему? Дело в том, что:\[{\upsilon _0} = \frac{S}{t} = S \cdot \frac{1}{t}\]Выражение \(\frac{1}{t}\) — это и есть перевернутая первая дробь.
Ответ верный, но в конце надо не умножать S * sqrt(g/2h), а делить.
Мы дробь под корнем перевернули, поэтому у нас умножение, а не деление, смотрите внимательнее