icodepro.ruУсловие задачи:
Камень массой 2 кг брошен вертикально вверх, его начальная кинетическая энергия 400 Дж. На какой высоте скорость камня будет равна 10 м/с?
Задача №2.8.13 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m=2\) кг, \(E_{к1}=400\) Дж, \(\upsilon=10\) м/с, \(h-?\)
Решение задачи:
При отсутствии неконсервативных сил, действующих на камень, например, силы сопротивления воздуха, полная механическая энергия камня сохраняется согласно закону сохранения энергии.
\[E = const\]
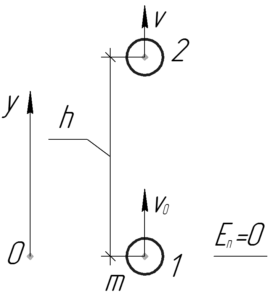
Возьмем нуль отсчета потенциальной энергии на уровне точки броска камня. Тогда понятно, что в точке 1 (смотрите схему) у камня имеется только кинетическая энергия \(E_{к1}\), а в точке 2 — и кинетическая \(E_{к2}\), и потенциальная \(E_{п2}\).
\[{E_{к1}} = {E_{к2}} + {E_{п2}}\]
Потенциальная и кинетическая энергии в точке 2 находятся по известным формулам, поэтому:
\[{E_{к1}} = \frac{{m{\upsilon ^2}}}{2} + mgh\]
Выразим из этого уравнения неизвестную высоту \(h\):
\[h = \frac{{2{E_{к1}} — m{\upsilon ^2}}}{{2mg}}\]
Так как все исходные данные задачи даны в системе СИ, то можно сразу посчитать ответ:
\[h = \frac{{2 \cdot 400 — 2 \cdot {{10}^2}}}{{2 \cdot 2 \cdot 10}} = 15\; м\]
Ответ: 15 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.8.12 Два шарика движутся навстречу друг другу со скоростями 1 и 0,5 м/с. После удара
2.8.14 Маленький шарик массой m, закрепленный на нерастяжимой нити в поле силы
2.8.15 Мальчик раскачивается на качелях. При максимальном отклонении от положения
Здравствуйте если масса будет не 2 а 3 то какой ответ получается
хороший ответ получается
У вас ошибка! В начальный момент времени полная энергия камня равна начальной кинетической энергии
В верхней точке подъема скорость камня равна 0, тогда и кинетическая энергия равна 0, тогда полная энергия равна конечной потенциальной энергии камня
Полная энергия, в отсутствие сопротивления воздуха, постоянна, поэтому E = m*g*h
h = E/(m*g) = 400/(2*10) = 20(м)
Ваши рассуждения, конечно, правильны, однако в задаче просят найти не максимальную высоту подъема, а высоту, на которой скорость тела будет равна 10 м/с. Согласно Вашим же рассуждениям, это не максимальная высота подъема.
А что такое g?
Это ускорение свободного падения, она равна 9,81 м/с2, но здесь мы использовали округленное до 10 м/с2 значение
Поправка к комментарию (14.11.2019 21:15): (v1^2-v2^2)/2g, а не (v2^2-v2^2)/2g
Исправил, спасибо!
А как в итоговой формуле получилость 2Ek1?
У меня выходит формула h=Ek1-mv^2/2mg
Смотрите: \[{E_{к1}} = \frac{{m{\upsilon ^2}}}{2} + mgh\] Умножаю на 2 обе части уравнения, тогда: \[2{E_{к1}} = m{\upsilon ^2} + 2mgh\] Оставляю \(2mgh\) в одной стороне, остальное переношу в другую: \[2{E_{к1}} — m{\upsilon ^2} = 2mgh\] Делю обе части на \(2mg\): \[h = \frac{{2{E_{к1}} — m{\upsilon ^2}}}{{2mg}}\]
В задаче написано что начальная кинетическая энергия равна 400 т.е потенциальная будет же равна 0 и т.к Eк=400 можно найти скорость и с помощью скорости через формулу (u1-u2)(u1+u2)/2g где u2=10 м/с можно найти высоту но получается 75м в чем ошибка?
При таком решении Вы должны были получить начальную скорость \(\upsilon_1 = 20\) м/с. Использую Вашу формулу:
\[h = \frac{\upsilon_2^2 — \upsilon_1^2}{2g} = \frac{20^2 — 10^2}{2 \cdot 10} = 15\;м\]
Вывод: где-то ошибаетесь в расчетах.