Условие задачи:

Катер проходит расстояние между двумя пунктами на реке в обе стороны за 14 ч. Чему равно это расстояние, если скорость катера в стоячей воде равна 35 км/ч, а скорость течения реки равна 5 км/ч?

Задача №1.7.12 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(T=14\) ч, \(\upsilon_к=35\) км/ч, \(\upsilon_т=5\) км/ч, \(S-?\)

Решение задачи:

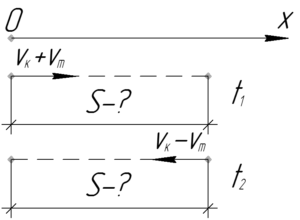Должно быть понятно, что скорость катера относительно берега при движении по течению реки равна \(\upsilon_к+\upsilon_т\), а при движении против течения — \(\upsilon_к -\upsilon_т\). Время \(T\), данное в условии, это сумма времени движения катера по течению \(t_1\) и против течения \(t_2\).

\[T = {t_1} + {t_2}\]

Так как движение катера было равномерным, а путь и туда, и обратно равен \(S\), то справедливо записать такую систему:

\[\left\{ \begin{gathered}
S = \left( {{\upsilon _к} + {\upsilon _т}} \right){t_1} \hfill \\
S = \left( {{\upsilon _к} — {\upsilon _т}} \right){t_2} \hfill \\
\end{gathered} \right.\]

Выразим время \(t_1\) и \(t_2\), подставим их в самое верхнее выражение:

\[\left\{ \begin{gathered}
{t_1} = \frac{S}{{{\upsilon _к} + {\upsilon _т}}} \hfill \\
{t_2} = \frac{S}{{{\upsilon _к} — {\upsilon _т}}} \hfill \\
\end{gathered} \right.\]

\[T = \frac{S}{{{\upsilon _к} + {\upsilon _т}}} + \frac{S}{{{\upsilon _к} — {\upsilon _т}}}\]

Правую часть равенства приведем под общий знаменатель.

\[T = \frac{{S\left( {{\upsilon _к} — {\upsilon _т}} \right) + S\left( {{\upsilon _к} + {\upsilon _т}} \right)}}{{\left( {{\upsilon _к} + {\upsilon _т}} \right)\left( {{\upsilon _к} — {\upsilon _т}} \right)}}\]

\[T = \frac{{S{\upsilon _к} — S{\upsilon _т} + S{\upsilon _к} + S{\upsilon _т}}}{{\upsilon _к^2 — \upsilon _т^2}}\]

\[T = \frac{{2S{\upsilon _к}}}{{\upsilon _к^2 — \upsilon _т^2}} \Rightarrow S = \frac{{T\left( {\upsilon _к^2 — \upsilon _т^2} \right)}}{{2{\upsilon _к}}}\]

Мы получили конечную формулу, остается только подсчитать ответ. Замечу, что можно не переводить данные в систему СИ, в таком случае мы получим ответ в километрах.

\[S = \frac{{14 \cdot \left( {{{35}^2} — {5^2}} \right)}}{{2 \cdot 35}} = 240\; км\]

Ответ: 240 км.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

1.7.11 В течение какого времени скорый поезд длиной 280 м, следуя со скоростью
1.7.13 Катер, переправляясь через реку шириной 600 м, двигался перпендикулярно
1.7.14 Когда нет ветра, капли дождя оставляют на окне равномерно движущегося вагона