Условие задачи:
Конькобежец движется по горизонтальному пути равномерно, а затем с разгона проезжает до остановки путь 60 м в течение 25 с. Масса конькобежца 50 кг. Определить мощность, затрачиваемую конькобежцем при равномерном движении.
Задача №2.7.49 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(S=60\) м, \(t=25\) с, \(m=50\) кг, \(N-?\)
Решение задачи:
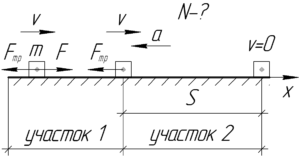 Искомую мощность конькобежца \(N\) при равномерном движении со скоростью \(\upsilon\) (участок 1) будем искать по формуле:
Искомую мощность конькобежца \(N\) при равномерном движении со скоростью \(\upsilon\) (участок 1) будем искать по формуле:
\[N = F \cdot \upsilon \;\;\;\;(1)\]
При равномерном движении на участке 1 сила тяги \(F\) равна силе трения скольжения \(F_{тр}\) (по первому закону Ньютона).
\[F = {F_{тр}}\;\;\;\;(2)\]
Последнюю будем искать из ускорения \(a\), с которым замедляется конькобежец на участке 2, по второму закону Ньютона (так как сила трения везде одинакова).
\[{F_{тр}} = ma\;\;\;\;(3)\]
Учитывая полученные выражения (2) и (3), формула (1) примет вид:
\[N = ma \cdot \upsilon \;\;\;\;(4)\]
Чтобы решить эту задачу, нужно найти ускорение \(a\) на участке замедления 2 и скорость \(\upsilon\), с которой конькобежец двигался до того, как стал тормозить под действием силы трения (участок 1). Так как конечная скорость равна нулю, то справедлива следующая формула:
\[\upsilon = at\;\;\;\;(5)\]
Запишем закон движения конькобежца на участке замедления:
\[S = \upsilon t — \frac{{a{t^2}}}{2}\]
Так как \(\upsilon = at\), то:
\[S = a{t^2} — \frac{{a{t^2}}}{2} = \frac{{a{t^2}}}{2}\]
\[a = \frac{{2S}}{{{t^2}}}\]
Тогда скорость \(\upsilon\) по формуле (5) равна:
\[\upsilon = \frac{{2S}}{t}\]
Полученные выражения для ускорения и скорости подставим в формулу (4), тем самым получив решение задачи в общем виде:
\[N = \frac{{2mS}}{{{t^2}}} \cdot \frac{{2S}}{t}\]
\[N = \frac{{4m{S^2}}}{{{t^3}}}\]
Произведем вычисление ответа:
\[N = \frac{{4 \cdot 50 \cdot {{60}^2}}}{{{{25}^3}}} = 46,08\;Вт\]
Ответ: 46,08 Вт.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.7.48 Допустим, что сила, которая заставляет баржу двигаться по каналу, прямо пропорциональна
2.7.50 Для растяжения недеформированной пружины на 1 см требуется сила, равная 30 Н
2.7.51 Шайба массы 0,1 кг, пущенная по льду с начальной скоростью 0,5 м/с, остановилась

 icodepro.ru
icodepro.ru
Как определить, когда нужно искать мгновенную мощность, а когда среднюю?
Думаю, что если при решении получится так, что средняя и мгновенные мощности отличаются, то Вам в условии обязательно скажут какую из них находить.
И ещё: мгновенная мощность обычно встречается в задачах на ускоренное движение.