Условие задачи:

Кубик совершает малые колебания в вертикальной плоскости, двигаясь без трения по внутренней поверхности сферической чаши. Определить период колебаний кубика, если радиус чаши 2,5 м.

Задача №9.2.21 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(R=2,5\) м, \(T-?\)

Решение задачи:

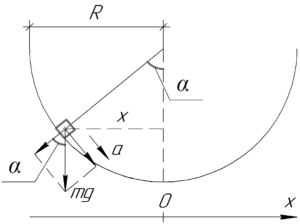Отклоним кубик по чаше на некоторый угол \(\alpha\). Если угол \(\alpha\) мал, то на кубик будет действовать возвращающая сила, равная \(mg \sin \alpha\). Запишем второй закон Ньютона:

\[mg\sin \alpha = ma\;\;\;\;(1)\]

Из рисунка к задаче видно, что синус угла \(\alpha\) можно определять по формуле:

\[\sin \alpha = — \frac{x}{R}\]

Синус получился отрицательным, так как отклонение \(x\) для положения кубика, показанного на рисунке — отрицательное.

Тогда формула (1) примет вид:

\[ — mg\frac{x}{R} = ma\]

Сократим обе части уравнения на массу \(m\) и запишем в следующем виде:

\[a + x\frac{g}{R} = 0\]

Из сравнения полученного уравнения с дифференциальным уравнением гармонических колебаний \(a + {\omega ^2}x = 0\) имеем:

\[{\omega ^2} = \frac{g}{R} \Rightarrow \omega = \sqrt {\frac{g}{R}} \]

Период колебаний \(T\) всегда можно найти по формуле:

\[T = \frac{{2\pi }}{\omega }\]

Поэтому окончательно получим:

\[T = 2\pi \sqrt {\frac{R}{g}} \]

Посчитаем численный ответ задачи:

\[T = 2 \cdot 3,14 \cdot \sqrt {\frac{{2,5}}{{10}}} = 3,14\;с\]

Ответ: 3,14 с.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

9.2.20 Математический маятник совершает колебания. В положении наибольшего отклонения
9.2.22 Небольшой металлический шарик массой 10 г, подвешенный на нити длиной 0,1 м
9.2.23 Математический маятник с длиной нити L совершает свободные колебания вблизи стены