icodepro.ruУсловие задачи:
Летящая пуля попадает в мешок с песком и углубляется на 15 см. На какую глубину войдет в песок такая же пуля, если её скорость увеличить вдвое? (Сила сопротивления постоянна, мешок неподвижен.)
Задача №2.1.35 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(S_1=15\) см, \(\upsilon_{02}=2\upsilon_{01}\), \(S_2-?\)
Решение задачи:
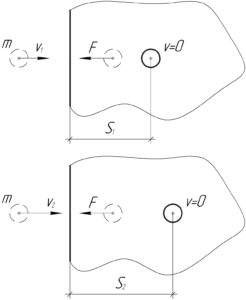Согласно теореме об изменении кинетической энергии применительно к этому случаю, работа силы сопротивления есть изменение кинетической энергии пули.
\[A = \Delta {W_к}\]
Работу силы сопротивления нужно находить как скалярное произведение вектора силы сопротивления и вектора перемещения.
\[A = \overrightarrow F \cdot \overrightarrow S \]
Так как эти вектора направлены в противоположные стороны, то есть угол между ними равен 180°, то это скалярное произведение распишется так:
\[A = FS\cos 180^\circ = — FS\]
Изменение кинетической энергии — это разность между конечной и начальной кинетическими энергиями.
\[\Delta {W_к} = {W_{к2}} — {W_{к1}}\]
В обоих случаях пуля останавливается, поэтому конечная кинетическая энергия равна нулю. Получается, что в этой задаче изменение кинетической энергии равно начальной кинетической энергии.
\[{W_{к2}} = 0 \Rightarrow \Delta {W_к} = — {W_{к1}}\]
В итоге:
\[ — FS = — {W_{к1}} \Rightarrow FS = {W_{к1}}\]
Кинетическая энергия пули, движущаяся со скоростью \(\upsilon\) равна:
\[W = \frac{{m{\upsilon ^2}}}{2}\]
Применительно к обоим описанным в условии случаям:
\[\left\{ \begin{gathered}
F{S_1} = \frac{{m\upsilon _{01}^2}}{2} \hfill \\
F{S_2} = \frac{{m\upsilon _{02}^2}}{2} \hfill \\
\end{gathered} \right.\]
Поделим нижнее выражение на верхнее:
\[\frac{{{S_2}}}{{{S_1}}} = \frac{{\upsilon _{02}^2}}{{\upsilon _{01}^2}}\]
Так как по условию \(\upsilon_{02}=2\upsilon_{01}\), то:
\[\frac{{{S_2}}}{{{S_1}}} = \frac{{4\upsilon _{01}^2}}{{\upsilon _{01}^2}} \Rightarrow \frac{{{S_2}}}{{{S_1}}} = 4 \Rightarrow {S_2} = 4{S_1}\]
\[{S_2} = 4 \cdot 15 = 60\; см\]
Ответ: 60 см.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.1.34 Канат может выдержать нагрузку 2,5 кН. С каким максимальным ускорением можно
2.1.36 Металлический шарик массой 100 г падает на горизонтальную плоскость с высоты 20 см
2.1.37 Мяч массой 0,15 кг ударяется о гладкую стенку под углом 30 градусов к ней
Можно проще: через формулу v0^2-v^2=-2aS (a=const, т к F сопр=const) приходим к тому же соотношению и находим S2
Да, можно решать и так. Это не проще, это практически тоже самое. Я решал через понятия динамики (энергия и работа), так как задача находится в теме «Динамика», а Вы — через кинематические понятия.
а можно решение ,которое попроще?
\[\left\{ \begin{gathered}
{\upsilon_{01} ^2} = 2a{S_1} \hfill \\
{\left( {2\upsilon_{01} } \right)^2} = 2a{S_2} \hfill \\
\end{gathered} \right.\]\[\left\{ \begin{gathered}
{\upsilon_{01} ^2} = 2a{S_1} \hfill \\
4{\upsilon_{01} ^2} = 2a{S_2} \hfill \\
\end{gathered} \right.\]\[\frac{{{S_2}}}{{{S_1}}} = 4\]
я не понимаю ,можно с объяснением что откуда,пожалуйста
В кинематике есть следующая формула, для равнозамедленного движения (в этом случае появляется минус в правой части) она выглядит так:\[\upsilon^2 — {\upsilon_0^2} = -2aS\]Здесь \(\upsilon\) — конечная скорость, \(\upsilon_0\) — начальная скорость, \(a\) — ускорение, \(S\) — путь (в данном случае). В нашем случае конечная скорость равна нулю (пуля остановится в мешке с песком), поэтому формула примет такой вид: \[\upsilon _0^2 = 2aS\]В первом случае начальная скорость равна \(\upsilon_{01}\), пройденный путь — \(S_1\), во втором начальная скорость равна \(2\upsilon_{01}\), пройденный путь — \(S_2\), поэтому:\[\left\{ \begin{gathered}
\upsilon _{01}^2 = 2a{S_1} \hfill \\
{\left( {2{\upsilon _{01}}} \right)^2} = 2a{S_2} \hfill \\
\end{gathered} \right.\]\[\left\{ \begin{gathered}
\upsilon _{01}^2 = 2a{S_1} \hfill \\
4\upsilon _{01}^2 = 2a{S_2} \hfill \\
\end{gathered} \right.\]Делим второе уравнение на первое почленно:\[\frac{{{S_2}}}{{{S_1}}} = 4\]