Условие задачи:
Люстра массой 10 кг висит на цепи, прочность которой 196 Н. На какой максимальный угол можно отклонить люстру от положения равновесия, чтобы при последующих качаниях люстры цепь не оборвалась? (\(g=9,8\) м/с2)
Задача №2.4.21 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m=10\) кг, \(T_{max}=196\) Н, \(g=9,8\) м/с2, \(\alpha_{max}-?\)
Решение задачи:
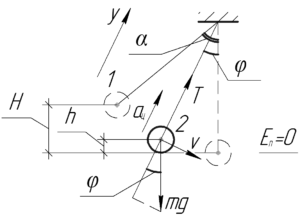 Решим задачу в общем виде. Пусть изначально люстру с цепью отклоняют на угол \(\alpha\), при этом требуется определить силу натяжения \(T\), когда цепь составляет с вертикалью угол \(\varphi\). Запишем для этого положения второй закон Ньютона в проекции на ось \(y\):
Решим задачу в общем виде. Пусть изначально люстру с цепью отклоняют на угол \(\alpha\), при этом требуется определить силу натяжения \(T\), когда цепь составляет с вертикалью угол \(\varphi\). Запишем для этого положения второй закон Ньютона в проекции на ось \(y\):
\[T — mg \cdot \cos \varphi = m{a_ц}\;\;\;\;(1)\]
Обозначим длину цепи равной \(l\). Пусть в этой точке скорость люстры равна \(\upsilon\), тогда центростремительное ускорение \(a_ц\) в этой точке найдем по формуле:
\[{a_ц} = \frac{{{\upsilon ^2}}}{l}\]
Тогда равенство (1) примет вид:
\[T — mg \cdot \cos \varphi = m\frac{{{\upsilon ^2}}}{l}\]
\[T = m\left( {g \cdot \cos \varphi + \frac{{{\upsilon ^2}}}{l}} \right)\;\;\;\;(2)\]
Также воспользуемся законом сохранения для положения 1 и 2:
\[mgH = mgh + \frac{{m{\upsilon ^2}}}{2}\]
Из схемы видно, что:
\[H = l\left( {1 — \cos \alpha } \right)\]
\[h = l\left( {1 — \cos \varphi } \right)\]
Тогда:
\[mgl\left( {1 — \cos \alpha } \right) = mgl\left( {1 — \cos \varphi } \right) + \frac{{m{\upsilon ^2}}}{2}\]
\[mgl\left( {\cos \varphi — \cos \alpha } \right) = \frac{{m{\upsilon ^2}}}{2}\]
\[{\upsilon ^2} = 2gl\left( {\cos \varphi — \cos \alpha } \right)\]
Полученное подставим в формулу (2):
\[T = m\left( {g \cdot \cos \varphi + \frac{{2gl\left( {\cos \varphi — \cos \alpha } \right)}}{l}} \right)\]
\[T = mg\left( {3\cos \varphi — 2\cos \alpha } \right)\]
Поработаем над этой формулой. Видно, что при любом фиксированном угле \(\alpha\), максимальная сила натяжения цепи наблюдается, когда косинус угла \(\varphi\) равен единице, т.е. угол \(\varphi\) равен 0°. Это момент, когда люстра проходит положение равновесия.
\[{T_{max}} = mg\left( {3 — 2\cos {\alpha _{max}}} \right)\]
\[3 — 2\cos {\alpha _{max}} = \frac{{{T_{max}}}}{{mg}}\]
\[{\alpha _{max}} = \arccos \left( {\frac{3}{2} — \frac{{{T_{max}}}}{{2mg}}} \right)\]
Задача решена в общем виде, теперь считаем ответ.
\[{\alpha _1} = \arccos \left( {\frac{3}{2} — \frac{{196}}{{2 \cdot 10 \cdot 9,8}}} \right) = 60^\circ = \frac{\pi }{3}\]
Ответ: \(\frac{\pi }{3}\).
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.4.20 Лыжник съезжает с вершины горы. На какой высоте от начала движения его давление
2.4.22 На легкой нерастяжимой нити подвешен тяжелый шарик. На какой угол нужно отвести
2.4.23 Нить может выдержать силу натяжения 25,4 Н. На нити подвесили тело массой 2 кг

 icodepro.ru
icodepro.ru