Условие задачи:
Минутная стрелка часов в 3 раза длиннее секундной. Во сколько раз линейная скорость конца секундной стрелки больше линейной скорости конца минутной стрелки?
Задача №1.8.10 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(R_2=3R_1\), \(T_1=1\) мин, \(T_2=1\) ч, \(\frac{\upsilon_1}{\upsilon_2}-?\)
Решение задачи:
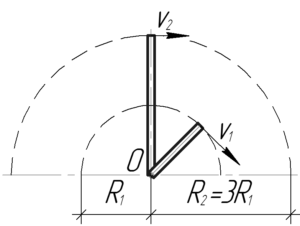 Дадим небольшое пояснение к условию задачи. Период, то есть время, за которое та или иная стрелка сделает полный оборот, у секундной стрелки равен \(T_1=1\) мин, а у минутной — \(T_2=1\) ч.
Дадим небольшое пояснение к условию задачи. Период, то есть время, за которое та или иная стрелка сделает полный оборот, у секундной стрелки равен \(T_1=1\) мин, а у минутной — \(T_2=1\) ч.
Линейную скорость конца любой стрелки можно определить по формуле:
\[\upsilon = \omega R\]
Циклическую частоту \(\omega\) определим по известной формуле, зная период \(T\):
\[\omega = \frac{{2\pi }}{T}\]
Суммируя все написанное:
\[\upsilon = \frac{{2\pi R}}{T}\]
Тогда отношение скоростей равно:
\[\frac{{{\upsilon _1}}}{{{\upsilon _2}}} = \frac{{2\pi {R_1} \cdot {T_2}}}{{{T_1} \cdot 2\pi {R_2}}} = \frac{{{R_1}{T_2}}}{{{R_2}{T_1}}}\]
Так как минутная стрелка длиннее секундной в 3 раза, то:
\[\frac{{{\upsilon _1}}}{{{\upsilon _2}}} = \frac{{{R_1}{T_2}}}{{3{R_1}{T_1}}} = \frac{{{T_2}}}{{3{T_1}}}\]
Подставим в эту формулу периоды в единицах СИ и получим ответ.
\[1\; ч = 3600\; с\]
\[1\; мин = 60\; с\]
\[\frac{{{\upsilon _1}}}{{{\upsilon _2}}} = \frac{{3600}}{{3 \cdot 60}} = 20\]
Ответ: в 20 раз.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.8.9 Колесо велосипеда делает 100 об/мин. Каков радиус колеса, если скорость
1.8.11 Тело движется по окружности с постоянной по модулю скоростью. Во сколько раз
1.8.12 Тело движется равномерно по окружности. Во сколько раз увеличится

 icodepro.ru
icodepro.ru
Потому что за один час минутная стрелка совершает полный оборот циферблата.
Т2 равен одному часу, потому что за 1 час минутная стрелка 5 раз пробежит циферблат, правильно?

Почему вместо т2 1 час
Потому что за один час минутная стрелка совершает полный оборот циферблата.