icodepro.ruУсловие задачи:
Мяч массой 0,15 кг ударяется о гладкую стенку под углом 30° к ней и отскакивает без потери скорости. Найти среднюю силу, действующую на мяч со стороны стенки, если скорость мяча 10 м/с, а продолжительность удара 0,1 с.
Задача №2.1.37 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m=0,15\) кг, \(\alpha=30^\circ\), \(\upsilon=10\) м/с, \(\Delta t=0,1\) с, \(F-?\)
Решение задачи:
Силу, действующую на мяч со сторонки стенки, можно найти, воспользовавшись вторым законом Ньютона, записанным в общем виде:
\[F = \frac{{\Delta p}}{{\Delta t}}\;\;\;\;(1)\]
В этой формуле \(\Delta p\) — это изменение импульса мяча вследствие удара о стенку, \(\Delta t\) — известное из условия время взаимодействия.
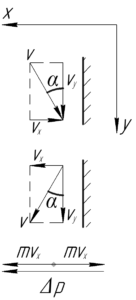
Найдем изменение импульса мяча. На рисунке изображены моменты непосредственно перед ударом и сразу после удара. Так как потерь скорости нет, то удар считается абсолютно упругим, поэтому мяч отскочит под тем же углом. Проецируем скорость мяча перед ударом и после удара на оси \(x\) и \(y\).
Видно, что по оси \(y\) проекции скорости \(\upsilon_y\) равны до и после удара \(\upsilon \cos \alpha\), поэтому изменения импульса мяча в этом направлении не было, а значит, в этом направлении и не действует сила.
По оси \(x\) модуль изменения импульса составит (смотри нижнюю часть схемы):
\[\Delta p = 2m{\upsilon _x} = 2m\upsilon \sin \alpha \;\;\;\;(2)\]
Подставим (2) в (1), получим решение задачи в общем виде.
\[F = \frac{{2m\upsilon \sin \alpha }}{{\Delta t}}\]
Подставляем данные задачи в эту формулу, считаем численный ответ.
\[F = \frac{{2 \cdot 0,15 \cdot 10 \cdot \sin 30^\circ }}{{0,1}} = 15\; Н\]
Ответ: 15 Н.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.1.36 Металлический шарик массой 100 г падает на горизонтальную плоскость с высоты 20 см
2.1.38 Вор, масса которого вместе с добычей 125 кг, убегая, налетает на камень. Столкновение
2.1.39 Два автомобиля с одинаковыми массами m движутся со скоростями v и 2v
Супер
Почему для изменения импульса мы берём Vx, а не Vy?
Потому что по оси \(y\) скорость (а значит и импульс) не изменяется
Нет. Мы должны брать по y. Т.к по х оно равно нулю. И разве не нужно брать cos30?
По оси \(y\) скорость не меняется ни по величине, ни по направлению, а вот по оси \(x\) изменяется по направлению. Скорость изменяется (по направлению) только по оси \(x\).
Горизонтальная проекция скорости есть противолежащий катет в прямоугольном треугольнике, поэтому нужно использовать синус.
Мяч массой m = 100 г ударяется о стену перпендикулярно поверхности стены и упруго отскакивает от нее. Скорость мяча до и после отскока v = 5 м / с. Каково среднее значение силы F, приложенной стенкой к мячу, если продолжительность столкновения t = 0,1 с?
p = 2*0.1*5 = 1
F = 1/0.1 = 10N
помогите с решением у меня нет угла в условии я должен игнорировать его в формуле или как-то найти?
В условии вашей задачи же сказано, что «ударяется о стену перпендикулярно», то есть \(\alpha=90^\circ\).
Почему 2mV?
Если вектор меняется свое направление на противоположное (как вектор импульса в этой задаче), то модуль его изменения равен двойному модулю начального (или конечного) вектора. Так получается по правилу вычитания векторов; как мы вычитали вектора также изображено на рисунке к решению задачи.
Почему v_x равен vsina ?
Смотрите на рисунок и проецируйте вектор на ось x, получите так же.
Спасибо, понял