icodepro.ruУсловие задачи:
На гладкой доске лежат два тела массами 2 и 3 кг, соединенные легкой нерастяжимой нитью. К первому телу приложили горизонтальную силу 5 Н, ко второму — 10 Н, направленную противоположно первой. Определите силу натяжения нити, соединяющей тела.
Задача №2.1.57 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m_1=2\) кг, \(m_2=3\) кг, \(F_1=5\) Н, \(F_2=10\) Н, \(T-?\)
Решение задачи:
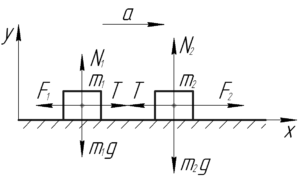Так как приложенные силы не равны по величине, то данная система тела начнет ускоренное движение в сторону большей силы. Из второго закона Ньютона в проекции на ось \(x\) для каждого из тел следует:
\[\left\{ \begin{gathered}
{F_2} — T = {m_2}a \hfill \\
T — {F_1} = {m_1}a \hfill \\
\end{gathered} \right.\]
Поделим выражения друг на друга.
\[\frac{{{F_2} — T}}{{T — {F_1}}} = \frac{{{m_2}}}{{{m_1}}}\]
Произведем математические преобразования целью которых является попытка выразить искомую силу натяжения \(T\). Перемножим дробь «крест-накрест»:
\[{F_2}{m_1} — T{m_1} = T{m_2} — {F_1}{m_2}\]
Все члены с \(T\) переносим в правую часть, выносим за скобки \(T\), выражаем \(T\).
\[T\left( {{m_1} + {m_2}} \right) = {F_2}{m_1} + {F_1}{m_2}\]
\[T = \frac{{{F_2}{m_1} + {F_1}{m_2}}}{{{m_1} + {m_2}}}\]
Посчитаем численное значение силы натяжения \(T\).
\[T = \frac{{10 \cdot 2 + 5 \cdot 3}}{{2 + 3}} = 7\; Н\]
Ответ: 7 Н.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.1.56 Чтобы на неподвижном блоке поднимать равномерно груз, требуется усилие 270 Н
2.1.58 Человек везет двое связанных между собой саней, прикладывая к веревке силу 120 Н
2.1.59 Тело массой 100 г движется вверх по вертикальной стенке под действием силы 2 Н
А почему мы не учитываем силу трения?
Два ящика соединенны веревкой. Масса первого ящика = 1 кг, масса второго ящика = 3 кг. На первый ящик действует горизонтально направленная сила= 10Н. Трение между коробками и поверхностью f = 0,2. С каким ускорением движутся блоки? Какой должен быть коэффициент трения, чтобы блоки двигались с постоянной скоростью?
помогите с решением плиз, у меня получилось по первому вопросу
a = 2.3с
а по второму вопросу ускорение получается нулевым, правильно? и коэффициент трения = 0,25
Если записать второй закон Ньютона для каждого тела в проекции на горизонтальную ось и сложить, то Вы должны получить:\[F — f\left( {M + m} \right)g = \left( {M + m} \right)a\]Откуда:\[a = \frac{F}{{M + m}} — fg\]\[a = \frac{{10}}{{3 + 1}} — 0,2 \cdot 10 = 0,5\;м/с^2\]Да, во втором случае ускорение нулевое. Записываете уже первый закон Ньютона для каждого тела в проекции на горизонтальную ось и складываете, тогда:\[f = \frac{F}{{\left( {M + m} \right)g}}\]\[f = \frac{{10}}{{\left( {3 + 1} \right) \cdot 10}} = 0,25\]Как видите, при нахождении ускорения у Вас где-то есть ошибка
У меня такой вопрос
Какой будет сила натяжения если силы F1 и F2 поменять местами?
Проделайте те же самые действия, тогда сможете ответить на свой же вопрос.
Записываем второй закон Ньютона для обоих тел:
\[\left\{ \begin{gathered}
{F_1} — T = — {m_2}a \hfill \\
T — {F_2} = — {m_1}a \hfill \\
\end{gathered} \right.\]
Делим уравнения друг на друга:
\[\frac{{{F_1} — T}}{{T — {F_2}}} = \frac{{{m_2}}}{{{m_1}}}\]
Перемножаем крест-накрест:
\[{F_1}{m_1} — T{m_1} = T{m_2} — {F_2}{m_2}\]
Все члены с \(T\) переносим в правую часть, выносим за скобки \(T\) и выражаем её.
\[T\left( {{m_1} + {m_2}} \right) = {F_1}{m_1} + {F_2}{m_2}\]
Откуда окончательно имеем:
\[T = \frac{{{F_1}{m_1} + {F_2}{m_2}}}{{{m_1} + {m_2}}}\]
Численный ответ:
\[T = \frac{{5 \cdot 2 + 10 \cdot 3}}{{2 + 3}} = 8\;Н\]
а ведь у нас между грузами возникает 2 силы натяжения в разные стороны. Нам не нужно их складывать?? (7+7)
Нет, нет и еще раз нет. На каждое из тел действует одна сила натяжения, так как на каждое тело действует одна нить. Сила натяжения возникает между каждым грузом и нитью, а не «между грузами».