Условие задачи:

На горизонтальной доске лежит брусок. Коэффициент трения скольжения между бруском и доской равен \(\mu\). Найти угол наклона доски к горизонтали, при котором сила трения покоя, действующая на брусок, будет максимальной?

Задача №2.3.22 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\mu\), \(\alpha-?\)

Решение задачи:

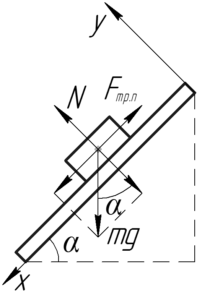Во-первых, если между бруском и доской действует сила трения покоя, то брусок ещё покоится. Во-вторых, если сила трения покоя примет максимальное значение, то её уже можно определять по формуле для силы трения скольжения (хотя брусок ещё не скользит). С учётом все сказанного, применим первый закон Ньютона в проекции на ось \(x\):

\[mg \cdot \sin \alpha  = {F_{тр.п}}\;\;\;\;(1)\]

Максимальная сила трения покоя определяется по формуле:

\[{F_{тр.п}} = \mu N\]

Чтобы определить силу реакции опоры запишем первый закон Ньютона в проекции на ось \(y\):

\[N = mg \cdot \cos \alpha \]

Тогда:

\[{F_{тр.п}} = \mu mg \cdot \cos \alpha \]

Подставим полученное в (1), а оттуда уже найдем искомый угол \(\alpha\).

\[mg \cdot \sin \alpha  = \mu mg \cdot \cos \alpha \]

\[tg\alpha  = \mu \]

\[\alpha  = arctg\mu \]

Ответ: \(arctg\;\mu\).

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.3.21 Груз поднимают с помощью ленточного транспортера, расположенного под углом
2.4.1 Мальчик массой 50 кг качается на качелях с длиной подвеса 4 м. С какой силой он давит
2.4.2 Автомобиль едет по выпуклому мосту, имеющему радиус кривизны 60 м. При какой