Условие задачи:

На горизонтальном дне водоема глубиной 1,2 м лежит плоское зеркало. На каком расстоянии от места вхождения луча в воду он снова выйдет на поверхность воды после отражения от зеркала? Угол падения луча на поверхность воды равен 30°.

Задача №10.3.8 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(h=1,2\) м, \(\alpha=30^\circ\), \(L-?\)

Решение задачи:

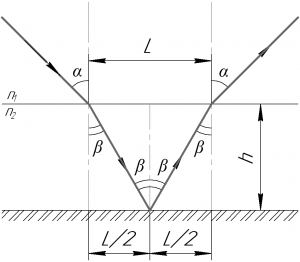Луч, который падает под углом \(\alpha\) к нормали к поверхности воды, войдя в воду, преломится, при этом угол преломления будет равен \(\beta\). Далее луч будет двигаться в толще воды, пока не отразится от зеркала, находящегося на дне водоема. Понятно, что угол падения луча на зеркало должен быть равен углу отражения. Потом луч также движется в воде под углом \(\beta\) к нормали к поверхности воды. При прохождении раздела сред наш луч опять преломится, при этом угол преломления будет уже равен \(\alpha\). Все описанное прекрасно видно на рисунке.

На рисунке видно, что искомое расстоянии от места вхождения луча в воду до места выхода луча из воды \(L\) можно найти из формулы:

\[tg\beta = \frac{L}{{2h}}\]

Откуда имеем:

\[L = 2h \cdot tg\beta \;\;\;\;(1)\]

Чтобы найти угол \(\beta\), запишем закон преломления света (также известен как закон преломления Снеллиуса):

\[{n_1}\sin \alpha = {n_2}\sin \beta \]

Здесь \(\alpha\) и \(\beta\) — угол падения и угол преломления соответственно, \(n_1\) и \(n_2\) — показатели преломления сред. Показатель преломления воздуха \(n_1\) равен 1, показатель преломления воды \(n_2\) равен 1,33.

Тогда:

\[\sin \beta = \frac{{{n_1}\sin \alpha }}{{{n_2}}}\]

\[\beta = \arcsin \left( {\frac{{{n_1}\sin \alpha }}{{{n_2}}}} \right)\;\;\;\;(2)\]

Подставим полученное выражение (2) в формулу (1):

\[L = 2h \cdot tg\left( {\arcsin \left( {\frac{{{n_1}\sin \alpha }}{{{n_2}}}} \right)} \right)\]

Задача решена в общем виде, посчитаем численный ответ:

\[L = 2 \cdot 1,2 \cdot tg\left( {\arcsin \left( {\frac{{1 \cdot \sin 30^\circ }}{{1,33}}} \right)} \right) = 0,974\;м = 97,4\;см\]

Ответ: 97,4 см.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

10.3.7 Луч света при переходе изо льда в воздух падает на поверхность льда под углом 15
10.3.9 Два взаимно перпендикулярных луча падают на поверхность воды. Угол падения
10.3.10 Водолазу, находящемуся под водой, кажется, что солнечные лучи падают под углом 60