Условие задачи:
На какой высоте находится аэростат, если с башни высотой 20 м он виден под углом 45° над горизонтом, а его изображение в озере видно под углом 60° под горизонтом?
Задача №10.1.10 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(h=20\) м, \(\alpha=45^\circ\), \(\beta=60^\circ\), \(H-?\)
Решение задачи:
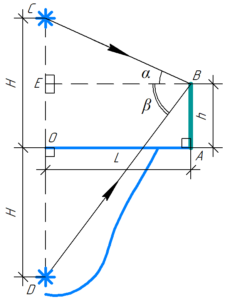 Для решения этой задачи необходимо сделать рисунок. Изобразим в виде отрезка AB высотой (длиной) \(h\) башню. Изобразим где-то в небе аэростат C, находящийся на искомой высоте \(H\) (длина отрезка CO) над озером. Покажем изображение аэростата в озере на глубине \(H\) (длина отрезка OD) от поверхности озера. Опустим из точки B (вершины башни) на отрезок CO перпендикуляр BE, длину которого обозначим за \(L\). Тогда получившийся на рисунке угол CBE — это данный в условии угол \(\alpha\), а угол DBE — это данный в условии угол \(\beta\).
Для решения этой задачи необходимо сделать рисунок. Изобразим в виде отрезка AB высотой (длиной) \(h\) башню. Изобразим где-то в небе аэростат C, находящийся на искомой высоте \(H\) (длина отрезка CO) над озером. Покажем изображение аэростата в озере на глубине \(H\) (длина отрезка OD) от поверхности озера. Опустим из точки B (вершины башни) на отрезок CO перпендикуляр BE, длину которого обозначим за \(L\). Тогда получившийся на рисунке угол CBE — это данный в условии угол \(\alpha\), а угол DBE — это данный в условии угол \(\beta\).
Рассмотрим два полученных прямоугольных треугольника CBE и DBE. Из рассмотрения имеем:
\[\left\{ \begin{gathered}
H — h = L \cdot tg\alpha \hfill \\
H + h = L \cdot tg\beta \hfill \\
\end{gathered} \right.\]
Чтобы избавиться от \(L\), разделим полученные уравнения друг на друга:
\[\frac{{H — h}}{{H + h}} = \frac{{tg\alpha }}{{tg\beta }}\]
Перемножим «крест-накрест», а потом раскроем скобки в обеих частях уравнения:
\[\left( {H + h} \right)tg\alpha = \left( {H — h} \right)tg\beta \]
\[H \cdot tg\alpha + h \cdot tg\alpha = H \cdot tg\beta — h \cdot tg\beta \]
Все слагаемые с \(h\) перенесем в левую часть, а с \(H\) — в правую:
\[h \cdot tg\alpha + h \cdot tg\beta = H \cdot tg\beta — H \cdot tg\alpha \]
Вынесем за скобки \(h\) и \(H\):
\[h\left( {tg\alpha + tg\beta } \right) = H\left( {tg\beta — tg\alpha } \right)\]
Окончательно получим такое решение задачи в общем виде:
\[H = \frac{{h\left( {tg\alpha + tg\beta } \right)}}{{tg\beta — tg\alpha }}\]
Посчитаем численный ответ задачи:
\[H = \frac{{20 \cdot \left( {tg45^\circ + tg60^\circ } \right)}}{{tg60^\circ — tg45^\circ }} = 74,64\;м\]
Ответ: 74,64 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
10.1.9 Небольшой предмет расположен между двумя плоскими зеркалами, образующими угол
10.1.11 Какова должна быть минимальная высота вертикального зеркала, в котором человек
10.1.12 Предмет помещен между двумя взаимно перпендикулярными зеркалами. Сколько

 icodepro.ru
icodepro.ru
Вот опять… Как учтено то, что луч идет из воздуха в воду?
Т.е. как учтено, что показатель преломления воды не равен показателю преломления воздуха?
Луч НЕ идет из глубин озера, преломляясь на границе фаз! В глубине находится изображение аэростата, а не сам аэростат. Я полагаю Вас смутила стрелка, показанная на рисунке, эту свою оплошность я исправлю.
благодарю