Решение: На p-V диаграмме изображен цикл, проводимый с одноатомным идеальным газом

Условие задачи:

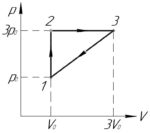На p-V диаграмме изображен цикл, проводимый с одноатомным идеальным газом. Чему равен коэффициент полезного действия этого цикла?

Задача №5.5.54 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\eta-?\)

Решение задачи:

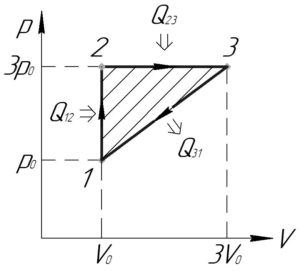Коэффициент полезного действия цикла \(\eta\) будем находить по формуле:

\[\eta = \frac{A}{{{Q_н}}}\;\;\;\;(1)\]

Работу цикла \(A\) численно равна площади фигуры цикла в координатах p-V, при этом если цикл обходится по часовой стрелке, то работа цикла будет положительной (как у нас). Фигура цикла представляет собой прямоугольный треугольник, поэтому:

\[A = \frac{1}{2}\left( {3{p_0} — {p_0}} \right)\left( {3{V_0} — {V_0}} \right)\]

\[A = 2{p_0}{V_0}\;\;\;\;(2)\]

Теперь нужно определить процессы в цикле, в которых теплота подводилась к газу. Запишем первый закон термодинамики:

\[Q = \Delta U + A\;\;\;\;(3)\]

Также запишем формулу для определения изменения внутренней энергии одноатомного идеального газа \(\Delta U\):

\[\Delta U = \frac{3}{2}\nu R\Delta T\;\;\;\;(4)\]

Запишем уравнение Клапейрона-Менделеева для точек 1-3:

\[\left\{ \begin{gathered}
{p_0}{V_0} = \nu R{T_1} \;\;\;\;(5)\hfill \\
3{p_0}{V_0} = \nu R{T_2} \;\;\;\;(6)\hfill \\
3{p_0} \cdot 3{V_0} = \nu R{T_3} \;\;\;\;(7)\hfill \\
\end{gathered} \right.\]

Рассмотрим изохорный процесс 1-2 (\(V=const\)), работа газа \(A_{12}\) в таком процессе равна нулю. Тогда количество теплоты \(Q_{12}\) по формуле (3), учитывая формулу (4), равно:

\[{Q_{12}} = \frac{3}{2}\nu R\Delta {T_{12}}\;\;\;\;(8)\]

Так как давление в процессе 1-2 растёт, значит растёт и температура, то есть \(\Delta T_{12}>0\). Поэтому, согласно формуле (8) \(Q_{12}>0\), то есть теплота в процессе 1-2 подводилась к газу. Учитывая формулы (5) и (6), формула (8) примет вид:

\[{Q_{12}} = \frac{3}{2}\left( {3{p_0}{V_0} — {p_0}{V_0}} \right) = 3{p_0}{V_0}\;\;\;\;(9)\]

Теперь рассмотрим изобарный процесс 2-3 (\(p=const\)). Работа газа \(A_{23}\) в таком процессе равна:

\[{A_{23}} = 3{p_0}\left( {3{V_0} — {V_0}} \right) = 3{p_0} \cdot 3{V_0} — 3{p_0}{V_0}\]

Учитывая уравнения (6) и (7), имеем:

\[{A_{23}} = \nu R\Delta {T_{23}}\]

Количество теплоты \(Q_{23}\) по формуле (3), учитывая формулу (4), равно:

\[{Q_{23}} = \frac{3}{2}\nu R\Delta {T_{23}} + \nu R\Delta {T_{23}}\]

\[{Q_{23}} = \frac{5}{2}\nu R\Delta {T_{23}}\;\;\;\;(10)\]

Так как объем в процессе 2-3 увеличивается, то по закону Гей-Люссака увеличивается и температура (\(\Delta T_{23}>0\)). Поэтому, согласно формуле (10) \(Q_{23}>0\), то есть теплота в процессе 2-3 к газу подводилась. Учитывая формулы (6) и (7), формула (10) примет вид:

\[{Q_{23}} = \frac{5}{2}\left( {3{p_0} \cdot 3{V_0} — 3{p_0}{V_0}} \right) = 15{p_0}{V_0}\;\;\;\;(11)\]

Так как в процессах 1-2 и 2-3 теплота подводится, значит в процессе 3-1 она отводится, так как хотя бы в одном из процессов цикла она должна отводится. Поэтому количество теплоты \(Q_н\), полученное от нагревателя, равно:

\[{Q_н} = {Q_{12}} + {Q_{23}}\]

Подставим в эту формулу выражения (9) и (11), тогда:

\[{Q_н} = 3{p_0}{V_0} + 15{p_0}{V_0}\]

\[{Q_н} = 18{p_0}{V_0}\;\;\;\;(12)\]

В формулу (1) для определения КПД \(\eta\) подставим выражения (2) и (12):

\[\eta = \frac{{2{p_0}{V_0}}}{{18{p_0}{V_0}}} = \frac{2}{{18}} = 0,111 = 11,1\% \]