icodepro.ruУсловие задачи:
На плоскопараллельную стеклянную пластинку толщиной 2 см под углом 60° падает луч света. Определить смещение луча на выходе из пластинки.
Задача №10.3.31 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(d=2\) см, \(\alpha=60^\circ\), \(l-?\)
Решение задачи:
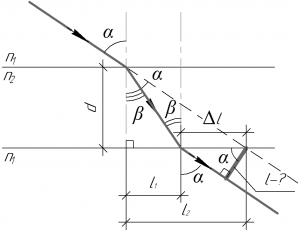Разумеется к такой задаче необходимо сделать хороший рисунок, без него решить задачу невозможно. Первое, что можно увидеть на рисунке, так это то, что искомое смещение \(l\) можно найти из прямоугольного треугольника по формуле:
\[l = \Delta l\cos \alpha\;\;\;\;(1)\]
Расстояние \(\Delta l\) можно определить следующим образом:
\[\Delta l = {l_2} — {l_1}\]
Расстояния \(l_1\) и \(l_2\) можно найти из соответствующих прямоугольных треугольников (да, опять) по следующим формулам:
\[\left\{ \begin{gathered}
{l_1} = d \cdot tg\beta \hfill \\
{l_2} = d \cdot tg\alpha \hfill \\
\end{gathered} \right.\]
Учитывая все вышесказанное, формула (1) примет вид:
\[l = d\cos \alpha \left( {tg\alpha — tg\beta } \right)\;\;\;\;(2)\]
Чтобы найти угол преломления \(\beta\), запишем закон преломления света (также известен как закон преломления Снеллиуса):
\[{n_1}\sin \alpha = {n_2}\sin \beta\]
Здесь \(\alpha\) и \(\beta\) — угол падения и угол преломления соответственно, \(n_1\) и \(n_2\) — показатели преломления сред. Показатель преломления воздуха \(n_1\) равен 1, показатель преломления стекла \(n_2\) равен 1,5.
Тогда:
\[\sin \beta = \frac{{{n_1}\sin \alpha }}{{{n_2}}}\]
\[\beta = \arcsin \left( {\frac{{{n_1}\sin \alpha }}{{{n_2}}}} \right)\;\;\;\;(3)\]
Подставим выражение (3) в формулу (2):
\[l = d\cos \alpha \left( {tg\alpha — tg\left( {\arcsin \left( {\frac{{{n_1}\sin \alpha }}{{{n_2}}}} \right)} \right)} \right)\]
Задача решена в общем виде, подставим данные задачи в полученную формулу и посчитаем численный ответ:
\[l = 0,02 \cdot \cos 60^\circ \left( {tg60^\circ — tg\left( {\arcsin \left( {\frac{{1 \cdot \sin 60^\circ }}{{1,5}}} \right)} \right)} \right) = 0,01\;м\]
Ответ: 0,01 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
10.3.30 Поверх стеклянной горизонтально расположенной пластины налит тонкий слой воды
10.3.32 На какое расстояние сместится луч, пройдя плоскопараллельную стеклянную пластинку
10.3.33 Определить смещение светового луча при прохождении его через стеклянную пластинку
Помогите пожалуйста с решением?
На плоскопараллельную стеклянную пластину толщиной 1 см падает луч света под углом 60 градусов. Часть света отражается от верхней, а часть — от нижней грани. Найти расстояние между соседними отраженными от пластины лучами. n= 1,5 (стекло)
СРОЧНО! ПОЖАЛУЙСТА, ПОМОГИТЕ С РЕШЕНИЕМ, ПРОШУ.
На плоскопараллельную стеклянную пластину толщиной d=2 см падает луч света под углом Часть света отражается, а часть, преломляясь, проходит в стекло, отражается от нижней поверхности и, преломляясь вторично, выходит в воздух параллельно первому отражённому лучу. Найти расстояние x между отражёнными лучами. Ответ выразить в мм округлив до целых. Показатели преломления воздуха и стекла равны n1=1 n2=1,5 и соответственно.
Из рисунка видно, что:\[x = l \cdot \sin \left( {90^\circ — \alpha } \right)\]\[x = l \cdot \cos \alpha \]Также:\[l = 2d \cdot tg\beta \]Поэтому:\[x = 2d \cdot tg\beta \cdot \cos \alpha \]Из закона преломления:\[{n_1}\sin \alpha = {n_2}\sin \beta \]Тогда:\[\beta = \arcsin \left( {\frac{{{n_1}\sin \alpha }}{{{n_2}}}} \right)\]В итоге решение задачи в общем виде такое:\[x = 2d \cdot tg\left( {\arcsin \left( {\frac{{{n_1}\sin \alpha }}{{{n_2}}}} \right)} \right) \cdot \cos \alpha \]Без численного значения угла падения посчитать численный ответ к задаче я Вам не смогу.