Условие задачи:

На поверхности водоема глубиной 5,3 м плавает круг радиусом 1 м, над центром которого на некоторой высоте $h$ расположен точечный источник света. Каково должно быть $h$, чтобы радиус тени от круга на дне водоема был максимальным? Найти этот радиус.

Задача №10.3.27 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$H=5,3$ м, $R=1$ м, $h-?$, $r-?$

Решение задачи:

Запишем закон преломления света (также известен как закон преломления Снеллиуса):

$${n_1}\sin \alpha = {n_2}\sin \beta\;\;\;\;(1)$$

Здесь $\alpha$ и $\beta$ — угол падения и угол преломления соответственно, $n_1$ и $n_2$ — показатели преломления сред. Показатель преломления воздуха $n_1$ равен 1, показатель преломления воды $n_2$ равен 1,33.

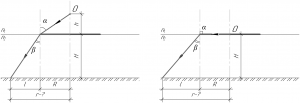
Радиус тени от круга на дне водоема будет тем больше, чем больше длина $l$ (смотрите рисунок слева), причем последняя будет тем больше, чем больше угол $\beta$. Из закона преломления (1) прекрасно видно, что углы $\alpha$ и $\beta$ находятся в прямой зависимости друг от друга, значит угол $\beta$ принимает максимальное значение, когда угол $\alpha$ равен 90°, то есть источник света расположен прямо на круге. Значит $h=0$.

Искомый радиус тени от круга на дне водоема $r$ можно найти по формуле (см. рисунок справа):

$$r = R + l\;\;\;\;(2)$$

Из прямоугольного треугольника:

$$l = H \cdot tg\beta\;\;\;\;(3)$$

Подставим выражение (3) в формулу (2):

$$r = R + H \cdot tg\beta$$

Из уравнения (1) найдем угол $\beta$:

$$\sin \beta = \frac{{{n_1}\sin \alpha }}{{{n_2}}}$$

$$\beta = \arcsin \left( {\frac{{{n_1}\sin \alpha }}{{{n_2}}}} \right)$$

Окончательно имеем:

$$r = R + H \cdot tg\left( {\arcsin \left( {\frac{{{n_1}\sin \alpha }}{{{n_2}}}} \right)} \right)$$

Посчитаем численный ответ:

$$r = 1 + 5,3 \cdot tg\left( {\arcsin \left( {\frac{{1 \cdot \sin 90^\circ }}{{1,33}}} \right)} \right) = 7,04\;м$$

Ответ: 0 м; 7,04 м.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

10.3.26 Кубический сосуд с непрозрачными стенками расположен так, что глаз наблюдателя
10.3.28 Луч света падает на стеклянную пластинку толщиной 3 см под углом 60°. Определить
10.3.29 Луч света падает под углом 40° на систему из трех плоскопараллельных стеклянных