Условие задачи:

Небольшое тело соскальзывает вниз по наклонному скату, переходящему в мертвую петлю радиусом 0,4 м. На какой высоте тело отрывается от петли, если начальная его высота 1 м?

Задача №2.8.48 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(R=0,4\) м, \(H=1\) м, \(h-?\)

Решение задачи:

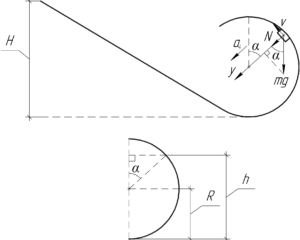Покажем тело на петле в произвольном положении, пусть при этом прямая, соединяющая центр петли и тело, составляет угол \(\alpha\) с вертикалью. Для этого положения запишем второй закон Ньютона в проекции на ось \(y\), которая проведена через вышеупомянутую прямую.

\[mg \cdot \cos \alpha  + N =  m{a_ц}\]

Общеизвестно, что центростремительное ускорение определяется по формуле:

\[{a_ц} = \frac{{{\upsilon ^2}}}{R}\]

Если в этом положении произойдет отрыв тела от петли, тогда сила реакции \(N\) в этой точке равна нулю. Поэтому:

\[mg \cdot \cos \alpha  = m\frac{{{\upsilon ^2}}}{R}\]

\[{\upsilon ^2} = gR \cdot \cos \alpha \;\;\;\;(1)\]

Интересно, что этот косинус можно найти из следующего выражения (смотрите нижнюю часть схемы):

\[\cos \alpha  = \frac{{h — R}}{R}\]

Тогда равенство (1) примет другой вид:

\[{\upsilon ^2} = g\left( {h — R} \right)\;\;\;\;(2)\]

Теперь запишем закон сохранения энергия — в начале у тела имелась только потенциальная энергия, в точке отрыва — и потенциальная, и кинетическая.

\[mgH = \frac{{m{\upsilon ^2}}}{2} + mgh\]

\[{\upsilon ^2} = 2g\left( {H — h} \right)\;\;\;\;(3)\]

Приравняем правые части равенств (2) и (3):

\[2g\left( {H — h} \right) = g\left( {h — R} \right)\]

\[2H — 2h = h — R\]

\[h = \frac{{2H + R}}{3}\]

Посчитаем численный ответ:

\[h = \frac{{2 \cdot 1 + 0,4}}{3} = 0,8\; м = 80\; см\]

Ответ: 80 см.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.8.47 Небольшое тело скользит с вершины полусферы вниз. На какой высоте h от вершины
2.8.49 Небольшое тело соскальзывает по наклонной плоскости, переходящей в мертвую
2.8.50 Плавательный бассейн площадью 100 м2 заполнен водой до глубины 2 м. Требуется