Условие задачи:
Объем пузырька, всплывающего на поверхность со дна озера, увеличился в два раза. Определить глубину озера. Температура воздуха на поверхности озера 27° C, а на его дне — 17° C. Атмосферное давление нормальное.
Задача №4.2.95 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(V_2=2V_1\), \(t_2=27^\circ\) C, \(t_1=17^\circ\) C, \(h-?\)
Решение задачи:
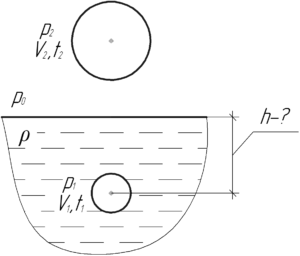 Давление воздуха внутри пузырька всегда равно внешнему давлению. Поэтому при нахождении пузырька на поверхности давление воздуха в нём \(p_2\) равно атмосферному давлению \(p_0\) (оно равно 100 кПа). Когда же пузырёк находился на дне озера, то давление воздуха в нём \(p_1\) больше атмосферного на величину гидростатического давлению воды высотой \(h\) (согласно закону Паскаля).
Давление воздуха внутри пузырька всегда равно внешнему давлению. Поэтому при нахождении пузырька на поверхности давление воздуха в нём \(p_2\) равно атмосферному давлению \(p_0\) (оно равно 100 кПа). Когда же пузырёк находился на дне озера, то давление воздуха в нём \(p_1\) больше атмосферного на величину гидростатического давлению воды высотой \(h\) (согласно закону Паскаля).
\[\left\{ \begin{gathered}
{p_1} = {p_0} + \rho gh \hfill \\
{p_2} = {p_0} \hfill \\
\end{gathered} \right.\]
Здесь \(\rho\) — плотность воды, равная 1000 кг/м3.
Применим объединённый газовый закон для воздуха, находящегося в пузырьке:
\[\frac{{{p_1}{V_1}}}{{{T_1}}} = \frac{{{p_2}{V_2}}}{{{T_2}}}\]
Учитывая равенства, приведённые выше в системе, получим:
\[\frac{{\left( {{p_0} + \rho gh} \right){V_1}}}{{{T_1}}} = \frac{{{p_0}{V_2}}}{{{T_2}}}\]
Тогда:
\[{p_0} + \rho gh = \frac{{{p_0}{V_2}{T_1}}}{{{V_1}{T_2}}}\]
\[\rho gh = {p_0}\left( {\frac{{{V_2}{T_1}}}{{{V_1}{T_2}}} — 1} \right)\]
\[h = \frac{{{p_0}}}{{\rho g}}\left( {\frac{{{V_2}{T_1}}}{{{V_1}{T_2}}} — 1} \right)\]
Согласно условию задачи объем всплывающего пузырька увеличился в два раза, то есть \(V_2=2V_1\), поэтому:
\[h = \frac{{{p_0}}}{{\rho g}}\left( {\frac{{2{V_1}{T_1}}}{{{V_1}{T_2}}} — 1} \right)\]
\[h = \frac{{{p_0}}}{{\rho g}}\left( {\frac{{2{T_1}}}{{{T_2}}} — 1} \right)\]
Переведём данные температуры в систему СИ:
\[27^\circ\;C = 300\;К\]
\[17^\circ\;C = 290\;К\]
Произведем вычисления:
\[h = \frac{{100 \cdot {{10}^3}}}{{1000 \cdot 10}}\left( {\frac{{2 \cdot 290}}{{300}} — 1} \right) = 9,33\;м\]
Ответ: 9,33 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
4.2.94 Горизонтально расположенный цилиндр разделен скользящей без трения перегородкой
4.2.96 Состояние одного киломоля идеального газа менялось по графику 1-2-3. Определить
4.2.97 Сосуд объемом 5 л разделен перегородкой на две части, заполненные одним газом

 icodepro.ru
icodepro.ru
откуда в скобках действие -1
h=p0?g(2V1T1V1T2—1)
h=p0?g(2T1T2—1)
в этой части решения ошибка
Я не вижу тут ошибки, конкретизируйте пожалуйста