Условие задачи:
Однородный куб плавает в воде, на 0,75 своего объема погрузившись в воду. Если тонкой вертикальной нитью прикрепить центр верхней грани куба к плечу рычага длиной 8 см, а на другой конец рычага длиной 4 см повесить гирю массой 30 г, то куб будет погружен в воду на 2/3 своего объема. Найти длину ребра куба.
Задача №3.3.47 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(V_{п1}=0,75V\), \(l_1=8\) см, \(l_2=4\) см, \(M=30\) г, \(V_{п2}=\frac{2}{3}V\), \(a-?\)
Решение задачи:
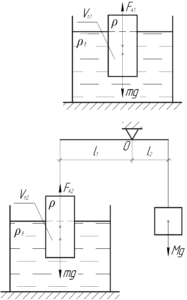 В начале куб плавает в воде, запишем условие плавания тел:
В начале куб плавает в воде, запишем условие плавания тел:
\[{F_{А1}} = mg\]
Распишем силу Архимеда и массу по формулам, тогда получим:
\[{\rho _в}g{V_{п1}} = \rho gV\]
Объем куба \(V\) можно найти как произведение длин всех трех ребер, т.е. \(V=a^3\). Учитывая, что \(V_{п1}=0,75V\), имеем:
\[{\rho _в}g \cdot 0,75{a^3} = \rho g{a^3}\]
\[\rho = 0,75{\rho _в}\]
Далее куб подвешивают к одному плечу рычага, а к другому — подвешивают гирю. Величина силы Архимеда, действующей на куб, изменится, так как изменится объем погруженной части. После этого рычаг будет находиться в равновесии. Запишем правило моментов (второе условие равновесия) относительно оси вращения рычага (точка O):
\[\left( {mg — {F_{А2}}} \right) \cdot {l_1} = Mg \cdot {l_2}\]
\[\left( {\rho Vg — {\rho _в}g{V_{п2}}} \right) \cdot {l_1} = Mg \cdot {l_2}\]
\[\left( {\rho V — \frac{2}{3}{\rho _в}V} \right) \cdot {l_1} = M \cdot {l_2}\]
\[\left( {\rho — \frac{2}{3}{\rho _в}} \right) \cdot V \cdot {l_1} = M \cdot {l_2}\]
Ранее мы определили, что \(V=a^3\) и \(\rho = 0,75{\rho _в}\):
\[\left( {0,75{\rho _в} — \frac{2}{3}{\rho _в}} \right) \cdot {a^3} \cdot {l_1} = M \cdot {l_2}\]
Домножим на 12 левую и правую часть равенства:
\[{\rho _в} \cdot {a^3} \cdot {l_1} = 12M \cdot {l_2}\]
\[a = \sqrt[3]{{\frac{{12M{l_2}}}{{{\rho _в}{l_1}}}}}\]
Переведем необходимые величины в систему СИ и посчитаем ответ:
\[8\;см = 0,08\;м\]
\[4\;см = 0,04\;м\]
\[30\;г = 0,03\;кг\]
\[a = \sqrt[3]{{\frac{{12 \cdot 0,03 \cdot 0,04}}{{1000 \cdot 0,08}}}} = 0,0564\;м \approx 56\;мм\]
Ответ: 56 мм.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
3.3.46 В воде плавает льдина с площадью поперечного сечения 5 м2 и высотой 0,5 м. Какую
3.3.48 Однородный пробковый брусок квадратного сечения со стороной 10 см и длиной 40 см
3.3.49 Однородный стержень длиной 1 м и площадью сечения 1 см2 плавает в вертикальном

 icodepro.ru
icodepro.ru
А почему во втором случае нет силы натяжении нити? Или эта сила не нужна?
Если совсем все подробно расписывать, то правило моментов можно записать в виде:\[{T_1}{l_1} = {T_2}{l_2}\]При этом силы натяжения можно найти так:\[\left\{ \begin{gathered}
{T_1} = mg — {F_{А2}} \hfill \\
{T_2} = Mg \hfill \\
\end{gathered} \right.\]Поэтому:\[\left( {mg — {F_{А2}}} \right){l_1} = Mg{l_2}\]