Решение: Определить число последовательно соединенных элементов с ЭДС 1,2 В и внутренним

Условие задачи:

Определить число последовательно соединенных элементов с ЭДС 1,2 В и внутренним сопротивлением 0,1 Ом каждый, если при подключении этой батареи к двум резисторам 6 и 9 Ом, соединенным параллельно, ток в цепи 3 А.

Задача №7.2.34 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\rm E=1,2\) В, \(r=0,1\) Ом, \(R_1=6\) Ом, \(R_2=9\) Ом, \(I=3\) А, \(N-?\)

Решение задачи:

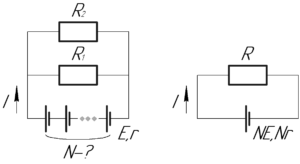Известно, что \(N\) последовательно соединенных источников с ЭДС, равной \(\rm E\), и внутренним сопротивлением, равным \(r\), можно заменить эквивалентным источником, у которого ЭДС будет равно \(N{\rm E}\), а внутреннее сопротивление — \(Nr\).

Учитывая это, найдем ток в цепи \(I\) по закону Ома для полной цепи:

\[I = \frac{{N{\rm E}}}{{R + Nr}}\]

Тогда:

\[N{\rm E} = IR + NIr\]

Все члены с искомым \(N\) перенесем в левую часть, где вынесем его за скобки.

\[N{\rm E} — NIr = IR\]

\[N\left( {{\rm E} — Ir} \right) = IR\]

\[N = \frac{{IR}}{{{\rm E} — Ir}}\]

Вообще \(R\) — это внешнее сопротивление цепи, равное в нашем случае эквивалентному сопротивлению двух параллельно соединенных резисторов \(R_1\) и \(R_2\):

\[R = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\]

Окончательно имеем:

\[N = \frac{{I{R_1}{R_2}}}{{\left( {{\rm E} — Ir} \right)\left( {{R_1} + {R_2}} \right)}}\]

Подставим данные задачи в формулу и посчитаем ответ:

\[N = \frac{{3 \cdot 6 \cdot 9}}{{\left( {1,2 — 3 \cdot 0,1} \right)\left( {6 + 9} \right)}} = 12\]