Решение: Определить разность потенциалов (по модулю) между точками, отстоящими

Условие задачи:

Определить разность потенциалов (по модулю) между точками, отстоящими от заряда 4 нКл на расстоянии 16 и 20 см.

Задача №6.3.11 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(q=4\) нКл, \(r_1=16\) см, \(r_2=20\) см, \(\Delta \varphi-?\)

Решение задачи:

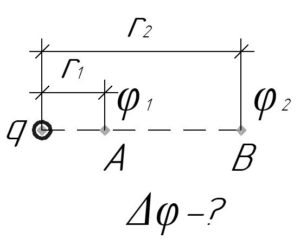Потенциал электрического поля заряда \(q\) в точке, находящей на некотором расстоянии \(r\) от указанного заряда, определяют так:

\[\varphi = \frac{{kq}}{r}\;\;\;\;(1)\]

Коэффициент пропорциональности \(k\) равен 9·10⁹ Н·м²/Кл².

Тогда потенциал в точках A и B можно найти соответственно по таким формулам:

\[\left\{ \begin{gathered}
{\varphi _1} = \frac{{kq}}{{{r_1}}} \hfill \\
{\varphi _2} = \frac{{kq}}{{{r_2}}} \hfill \\
\end{gathered} \right.\]

Из формулы (1) видно, что чем дальше находится точка, в которой определяют потенциал, тем потенциал меньше (так как \({r_1} < {r_2}\), то \({\varphi_1} > {\varphi_2}\)). Поэтому модуль разности потенциалов \(\Delta \varphi\) следует искать, используя такую формулу:

\[\Delta \varphi = {\varphi _1} — {\varphi _2}\]

Учитывая формулы из вышеприведённой системы, имеем:

\[\Delta \varphi = \frac{{kq}}{{{r_1}}} — \frac{{kq}}{{{r_2}}}\]

Напоследок приведём формулу под общий знаменатель:

\[\Delta \varphi = \frac{{kq\left( {{r_2} — {r_1}} \right)}}{{{r_1}{r_2}}}\]

Произведём вычисления:

\[\Delta \varphi = \frac{{9 \cdot {{10}^9} \cdot 4 \cdot {{10}^{ — 9}} \cdot \left( {0,2 — 0,16} \right)}}{{0,16 \cdot 0,2}} = 45\;В\]