Условие задачи:
Определить скорость относительно берега реки лодки, идущей перпендикулярно к течению. Скорость течения реки 1 м/с, скорость лодки относительно воды 2 м/с.
Задача №1.7.1 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\upsilon_0=1\) м/с, \(\upsilon_1=2\) м/с, \(\upsilon-?\)
Решение задачи:
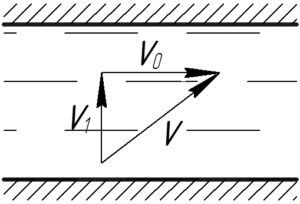 Перед нами классическая задача на относительность движения, а точнее на применение правила сложения скоростей. Оно гласит, что скорость тела (лодки в нашем случае) относительно неподвижной системы отсчета (берега) \(\upsilon\) есть векторная сумма скорости тела относительно подвижной системы отсчета (реки) \(\upsilon_1\) и скорость самой подвижной системы отсчета (скорость течения реки) \(\upsilon_0\).
Перед нами классическая задача на относительность движения, а точнее на применение правила сложения скоростей. Оно гласит, что скорость тела (лодки в нашем случае) относительно неподвижной системы отсчета (берега) \(\upsilon\) есть векторная сумма скорости тела относительно подвижной системы отсчета (реки) \(\upsilon_1\) и скорость самой подвижной системы отсчета (скорость течения реки) \(\upsilon_0\).
\[\overrightarrow \upsilon = \overrightarrow {{\upsilon _1}} + \overrightarrow {{\upsilon _0}} \]
По рисунку к задаче видно, что скорости \(\upsilon_0\) и \(\upsilon_1\) перпендикулярны друг к другу, поэтому искомую скорость \(\upsilon\) можно найти из теоремы Пифагора.
\[\upsilon = \sqrt {\upsilon _1^2 + \upsilon _0^2} \]
Сосчитаем ответ, подставив в формулу численные значения.
\[\upsilon = \sqrt {{2^2} + {1^2}} = 2,24\; м/с = 8,05\; км/ч\]
Ответ: 8,05 км/ч.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.6.22 Тело брошено под углом 60 к горизонту с начальной скоростью
1.7.2 Скорость течения реки 1,5 м/с. Какую скорость относительно воды должен иметь
1.7.3 Движение двух автомобилей по шоссе задано уравнениями x1=2t+0,2t^2 и x2=80-4t

 icodepro.ru
icodepro.ru
Почему по теореме пифагора? не могу понять..