Условие задачи:
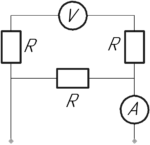 Определите показание амперметра в электрической цепи, изображенной на рисунке, если показание вольтметра \(U=250\) В, а сопротивление каждого резистора \(R\) и внутреннее сопротивление вольтметра равны по 1 кОм.
Определите показание амперметра в электрической цепи, изображенной на рисунке, если показание вольтметра \(U=250\) В, а сопротивление каждого резистора \(R\) и внутреннее сопротивление вольтметра равны по 1 кОм.
Задача №7.5.50 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(U=250\) В, \(R=1\) кОм, \(I-?\)
Решение задачи:
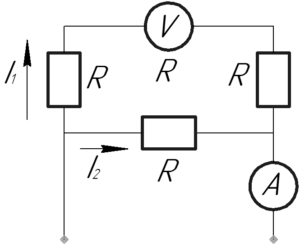 Так как из условия задачи нам известно показание вольтметра \(U\), то зная внутреннее сопротивление вольтметра, а оно такое же, как у резисторов, то есть равно \(R\), очень легко определить ток \(I_1\), который течет по верхней ветви, благодаря закону Ома для участка цепи:
Так как из условия задачи нам известно показание вольтметра \(U\), то зная внутреннее сопротивление вольтметра, а оно такое же, как у резисторов, то есть равно \(R\), очень легко определить ток \(I_1\), который течет по верхней ветви, благодаря закону Ома для участка цепи:
\[I_1 = \frac{U}{R}\;\;\;\;(1)\]
Очевидно, что верхняя ветвь, состоящая из последовательно соединенных двух резисторов и вольтметра (все имеющие одинаковое сопротивление \(R\)), и нижняя ветвь, состоящая из одного резистора, соединены параллельно, то они находятся под одинаковым напряжением, поэтому верно записать:
\[{I_1} \cdot 3R = {I_2} \cdot R\]
Откуда имеем:
\[{I_2} = 3{I_1}\]
\[{I_2} = \frac{{3U}}{R}\;\;\;\;(2)\]
Очевидно, что ток \(I\), который показывает амперметр, равен сумме токов \(I_1\) и \(I_2\), то есть:
\[I = {I_1} + {I_2}\]
Учитывая выражения (1) и (2), имеем:
\[I = \frac{U}{R} + \frac{{3U}}{R}\]
\[I = \frac{{4U}}{R}\]
Посчитаем численный ответ:
\[I = \frac{{4 \cdot 250}}{{1 \cdot {{10}^3}}} = 1\;А\]
Ответ: 1 А.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
7.5.49 Вольтметр, внутреннее сопротивление которого равно 50 кОм, подключенный к источнику
7.5.51 Какой величины надо взять дополнительное сопротивление, чтобы можно было включить
7.1.1 Определить силу тока, проходящего через сопротивление 15 Ом, если напряжение на нем

 icodepro.ru
icodepro.ru
А почему решение «стандартным» методом не работает? То есть если я найду общее сопротивление участка (750 Ом) и поделю напряжение (250 В) на это сопротивление, ответ правильным не будет. Почему так?
Потому что вольтметр показывает падение напряжения на своем внутреннем сопротивлении (т.е. после первого резистора и перед вторым, если считать первым и вторым резисторами верхние по схеме резисторы).
Вы неправильно считаете, что он показывает напряжение между узлами схемы (т.е. где ток разделяется на \(I_1\) и \(I_2\) и потом соединяется).