Условие задачи:
От предмета высотой 20 см при помощи линзы получили действительное изображение предмета высотой 80 см. Когда предмет передвинули на 5 см, то получили действительное изображение высотой 40 см. Найти оптическую силу линзы.
Задача №10.5.56 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(h=20\) см, \(H_1=80\) см, \(\Delta d=5\) см, \(H_2=40\) см, \(D-?\)
Решение задачи:
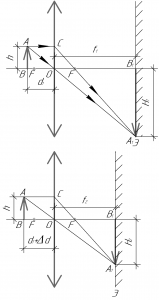 Так как c помощью линзы получают действительное изображение пламени свечи на экране, значит мы имеем дело с собирающей линзой, поскольку рассеивающая линза не может давать такого изображения. При этом расстояние от свечи до линзы в обоих случаях должно быть больше фокусного расстояния, т.е. свеча находится левее заднего фокуса линзы (см. рисунки к задаче). Кстати, предмет отодвигали от линзы, то есть расстояние от предмета до линзы увеличивалось, так как изображение предмета увеличивалось.
Так как c помощью линзы получают действительное изображение пламени свечи на экране, значит мы имеем дело с собирающей линзой, поскольку рассеивающая линза не может давать такого изображения. При этом расстояние от свечи до линзы в обоих случаях должно быть больше фокусного расстояния, т.е. свеча находится левее заднего фокуса линзы (см. рисунки к задаче). Кстати, предмет отодвигали от линзы, то есть расстояние от предмета до линзы увеличивалось, так как изображение предмета увеличивалось.
Запишем формулу тонкой линзы для собирающей линзы для случая, когда линза дает действительное изображение:
\[D = \frac{1}{d} + \frac{1}{f}\;\;\;\;(1)\]
В этой формуле \(D\) — оптическая силы линзы, это положительная величина, поскольку линза — собирающая, \(d\) — расстояние от линзы до предмета, знак перед ним «+», поскольку предмет — действительный (в случае одиночной линзы предмет всегда действительный, оно бывает мнимым в случае системы линз), \(f\) — расстояние от линзы до изображения, знак перед ним «+», поскольку изображение — действительное (то есть образуется на сходящемся пучке лучей — смотрите рисунок).
Запишем формулу (1) для двух случаев, описанных в условии задачи:
\[\left\{ \begin{gathered}
D = \frac{1}{{{d_1}}} + \frac{1}{{{f_1}}} \;\;\;\;(2)\hfill \\
D = \frac{1}{{{d_1} + \Delta d}} + \frac{1}{{{f_2}}} \hfill \\
\end{gathered} \right.\]
Из подобия треугольников AOB и A1OB1 по трем углам на обоих рисунках получим следующие равенства:
\[\left\{ \begin{gathered}
\frac{{{H_1}}}{h} = \frac{{{f_1}}}{{{d_1}}} \hfill \\
\frac{{{H_2}}}{h} = \frac{{{f_2}}}{{{d_1} + \Delta d}} \hfill \\
\end{gathered} \right.\]
Здесь \(h\) — высота пламени свечи, \(H_1\) и \(H_2\) — высота соответствующих изображений пламени свечи.
Отсюда выразим расстояния от линзы до изображения (экрана) \(f_1\) и \(f_2\):
\[\left\{ \begin{gathered}
{f_1} = \frac{{{H_1}{d_1}}}{h} \;\;\;\;(3)\hfill \\
{f_2} = \frac{{{H_2}\left( {{d_1} + \Delta d} \right)}}{h} \hfill \\
\end{gathered} \right.\]
С учетом этого вышеприведенная система уравнений примет такой вид:
\[\left\{ \begin{gathered}
D = \frac{1}{{{d_1}}} + \frac{h}{{{H_1}{d_1}}} \hfill \\
D = \frac{1}{{{d_1} + \Delta d}} + \frac{h}{{{H_2}\left( {{d_1} + \Delta d} \right)}} \hfill \\
\end{gathered} \right.\]
Приведем под общий знаменатель в правых частях обоих уравнений:
\[\left\{ \begin{gathered}
D = \frac{{{H_1} + h}}{{{H_1}{d_1}}} \hfill \\
D = \frac{{{H_2} + h}}{{{H_2}\left( {{d_1} + \Delta d} \right)}} \hfill \\
\end{gathered} \right.\]
Тогда имеем такое уравнение:
\[\frac{{{H_1} + h}}{{{H_1}{d_1}}} = \frac{{{H_2} + h}}{{{H_2}\left( {{d_1} + \Delta d} \right)}}\]
Перемножим «крест-накрест»:
\[{H_1}{d_1}\left( {{H_2} + h} \right) = {H_2}\left( {{H_1} + h} \right)\left( {{d_1} + \Delta d} \right)\]
Раскроем скобки в обеих частях уравнения:
\[{H_1}{H_2}{d_1} + {H_1}{d_1}h = {H_1}{H_2}{d_1} + {H_1}{H_2}\Delta d + {H_2}h{d_1} + {H_2}h\Delta d\]
\[{H_1}{d_1}h = {H_1}{H_2}\Delta d + {H_2}h{d_1} + {H_2}h\Delta d\]
\[{H_1}{d_1}h — {H_2}h{d_1} = {H_1}{H_2}\Delta d + {H_2}h\Delta d\]
\[{d_1}h\left( {{H_1} — {H_2}} \right) = \Delta d{H_2}\left( {{H_1} + h} \right)\]
\[{d_1} = \frac{{\Delta d{H_2}\left( {{H_1} + h} \right)}}{{h\left( {{H_1} — {H_2}} \right)}}\;\;\;\;(4)\]
Также, учитывая (3), получим:
\[{f_1} = \frac{{\Delta d{H_1}{H_2}\left( {{H_1} + h} \right)}}{{{h^2}\left( {{H_1} — {H_2}} \right)}}\;\;\;\;(5)\]
Принимая во внимание полученные выражения (4) и (5), уравнение (2) примет вид:
\[D = \frac{{h\left( {{H_1} — {H_2}} \right)}}{{\Delta d{H_2}\left( {{H_1} + h} \right)}} + \frac{{{h^2}\left( {{H_1} — {H_2}} \right)}}{{\Delta d{H_1}{H_2}\left( {{H_1} + h} \right)}}\]
Приведем в правой части под общий знаменатель:
\[D = \frac{{h{H_1}\left( {{H_1} — {H_2}} \right) + {h^2}\left( {{H_1} — {H_2}} \right)}}{{\Delta d{H_1}{H_2}\left( {{H_1} + h} \right)}}\]
\[D = \frac{{h\left( {{H_1} — {H_2}} \right)\left( {{H_1} + h} \right)}}{{\Delta d{H_1}{H_2}\left( {{H_1} + h} \right)}}\]
Окончательно получим следующее решение задачи в общем виде:
\[D = \frac{{h\left( {{H_1} — {H_2}} \right)}}{{\Delta d{H_1}{H_2}}}\]
Посчитаем численный ответ:
\[D = \frac{{0,2 \cdot \left( {0,8 — 0,4} \right)}}{{0,05 \cdot 0,8 \cdot 0,4}} = 5\;дптр\]
Ответ: 5 дптр.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
10.5.55 Расстояние от предмета до линзы и от линзы до изображения предмета одинаковы
10.5.57 Предмет расположен перпендикулярно оптической оси собирающей линзы. На сколько
10.5.58 Точечный источник света находится на расстоянии 40 см от собирающей линзы

 icodepro.ru
icodepro.ru