Условие задачи:
Пассажирский поезд идет со скоростью 72 км/ч. По соседнему пути движется навстречу ему товарный поезд длиной 140 м со скоростью 54 км/ч. Сколько времени человек, стоящий у окна, будет видеть проходящий мимо него товарный поезд?
Задача №1.7.18 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\upsilon_1=72\) км/ч, \(L_2=140\) м, \(\upsilon_2=54\) км/ч, \(t-?\)
Решение задачи:
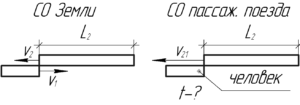 Перейдем в систему отсчета (СО), связанную с пассажирским поездом. Модуль скорости товарного поезда в этой СО равен сумме скоростей поездов относительно Земли. Вы можете сами удостовериться в этом, применив правило сложения скоростей (точнее правило, обратное ему).
Перейдем в систему отсчета (СО), связанную с пассажирским поездом. Модуль скорости товарного поезда в этой СО равен сумме скоростей поездов относительно Земли. Вы можете сами удостовериться в этом, применив правило сложения скоростей (точнее правило, обратное ему).
\[{\upsilon _{21}} = {\upsilon _1} + {\upsilon _2}\]
Мимо человек товарный поезд длиной \(L_2\) будет проноситься равномерно со скоростью \(\upsilon_{21}\), поэтому человек будет видеть его время \(t\), определяемое по формуле:
\[t = \frac{{{L_2}}}{{{\upsilon _{21}}}} = \frac{{{L_2}}}{{{\upsilon _1} + {\upsilon _2}}}\]
Переведем скорости поездов в систему СИ, то есть в м/с.
\[72\; км/ч = \frac{{72 \cdot 1000}}{{1 \cdot 3600}}\; м/с = \frac{{720}}{{36}}\; м/с = 20\; м/с\]
\[54\; км/ч = \frac{{54 \cdot 1000}}{{1 \cdot 3600}}\; м/с = \frac{{540}}{{36}}\; м/с = 15\; м/с\]
Тогда численный ответ равен:
\[t = \frac{{140}}{{20 + 15}} = 4\; с\]
Ответ: 4 с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.7.17 Пловец переплывает реку по прямой, перпендикулярной берегу. Определить
1.7.19 Парашютист опускается вертикально вниз со скоростью 4 м/с в безветренную погоду
1.7.20 Вертолет летит на высоте 500 м со скоростью 100 м/с. Навстречу ему по реке

 icodepro.ru
icodepro.ru
По идее, такая же задача, как 1.7.16.
Верно!
Очень много задач одинаковы по способу решения
Почему время определяется отношением длины к сумме скоростей, а не наоборот?
Потому что S=vt, откуда t=S/v