icodepro.ruУсловие задачи:
Первую половину пути велосипедист проехал со скоростью в 8 раз большей, чем вторую. Средняя скорость велосипедиста оказалось равной 16 км/ч. Определить скорость велосипедиста на второй половине пути.
Задача №1.2.11 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(S_1=S_2=\frac{1}{2}S\), \(\upsilon_1=8\upsilon_2\), \(\upsilon_{ср}=16\) км/ч, \(\upsilon_2-?\)
Решение задачи:
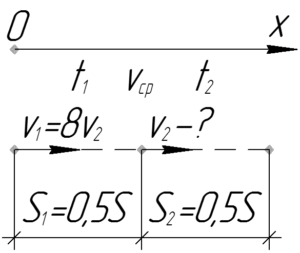Среднюю скорость велосипедиста можно найти как отношение всего пути к затраченному на все движение времени. Так как весь путь \(S\) состоит из двух участков, то запишем:
\[{\upsilon _{ср}} = \frac{{{S_1} + {S_2}}}{{{t_1} + {t_2}}}\]
Движение везде было равномерным, поэтому найдем время \(t_1\) и \(t_2\) таким образом:
\[\left\{ \begin{gathered}
{t_1} = \frac{{{S_1}}}{{{\upsilon _1}}} \hfill \\
{t_2} = \frac{{{S_2}}}{{{\upsilon _2}}} \hfill \\
\end{gathered} \right.\]
По условию \(S_1=S_2=\frac{1}{2}S\) и \(\upsilon_1=8\upsilon_2\), поэтому:
\[\left\{ \begin{gathered}
{t_1} = \frac{S}{{2{\upsilon _1}}} = \frac{S}{{16{\upsilon _2}}} \hfill \\
{t_2} = \frac{S}{{2{\upsilon _2}}} \hfill \\
\end{gathered} \right.\]
Подставим выражения в формулу средней скорости.
\[{\upsilon _{ср}} = \frac{S}{{\frac{S}{{16{\upsilon _2}}} + \frac{S}{{2{\upsilon _2}}}}} = \frac{S}{{\frac{{9S}}{{16{\upsilon _2}}}}} = \frac{{S \cdot 16{\upsilon _2}}}{{9S}} = \frac{{16{\upsilon _2}}}{9}\]
В итоге конечная формула для нахождения \(\upsilon_2\) имеет вид:
\[{\upsilon _2} = \frac{{9{\upsilon _{ср}}}}{{16}}\]
Вычислим ответ.
\[{\upsilon _2} = \frac{{9 \cdot 16}}{{16}} = 9\; км/ч = 2,5\; м/с\]
Ответ: 2,5 м/с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.2.10 Тело первую половину пути двигалось со скоростью 12 км/ч. После этого половину
1.2.12 Мотоциклист за первые 5 минут проехал 3 км, за последующие 8 минут — 9,6 км и
1.2.13 Автобус прошел первые 4 км со средней скоростью 20 км/ч, а следующие 0,3 ч он
Спасибо огромное за решение задачи
Огромное спасибо за решение! Очень помогло, красиво оформлено а главное понятно!
Не понятно откуда взялось 9S, в выражении средней скорости?
В знаменателе я складываю две дроби. Чтобы сложить две дроби, их нужно привести под общий знаменатель:\[\frac{S}{{16{\upsilon _2}}} + \frac{S}{{2{\upsilon _2}}} = \frac{S}{{16{\upsilon _2}}} + \frac{{8S}}{{16{\upsilon _2}}} = \frac{{S + 8S}}{{16{\upsilon _2}}} = \frac{{9S}}{{16{\upsilon _2}}}\]
не очень поняла как Вы нашли конечную формулу
\[{t_1} + {t_2} = \frac{S}{{16{\upsilon _2}}} + \frac{S}{{2{\upsilon _2}}} = \frac{{9S}}{{16{\upsilon _2}}}\]Полученную формулу подставляю в знаменатель этой формулы:\[{\upsilon _{ср}} = \frac{S}{{{t_1} + {t_2}}}\]Тогда имеем:\[{\upsilon _{ср}} = \frac{{S \cdot 16{\upsilon _2}}}{{9S}} = \frac{{16{\upsilon _2}}}{9}\]Отсюда остается только выразить искомую \(\upsilon_2\):\[{\upsilon _2} = \frac{{9{\upsilon _{ср}}}}{{16}}\]
Здравствуйте, есть подобным пример под номером (1.2.9) и перечитав условие задачи, я нашел несхожесть. В примере (1.2.9):
Средняя скорость на всем пути составила 4 км/ч, а в этом Средняя скорость велосипедиста оказалось равной 16 км/ч, если не сложно можете обьяснить в чем различие, которая меняет последние формулы?
Различие в том, что в этих задачах разное отношение скоростей на первом и втором участках, это и меняет цифры в дроби окончательной формулы.
Вообще можно решить задачу в общем виде, когда первую половину пути проезжают со скоростью в \(n\) раз большей, чем вторую. Попробуйте, потренируйтесь, ничего сложно в этом нет.
спасибо огромное